第 8 课：卷积神经网络

在计算机视觉中有一个问题，就是输入的数据可能会很大。
我们之前讲到的神经网络连接方式都叫做 “全连接”，而我们之前用的都是64 * 64 * 3 的小图片，所以还没什么问题
但是当图片尺寸比较大时，就很难处理，比如 1000 * 1000 * 3
因此我们需要使用 卷积计算

（一）卷积计算

计算机视觉最底层的原理是边缘检测， 这个我们在之前就已经讲到过
前面几层检测边缘，中间的层检测部分区域，后面的层检测完整物体

更细化一点，要分为垂直边缘和水平边缘

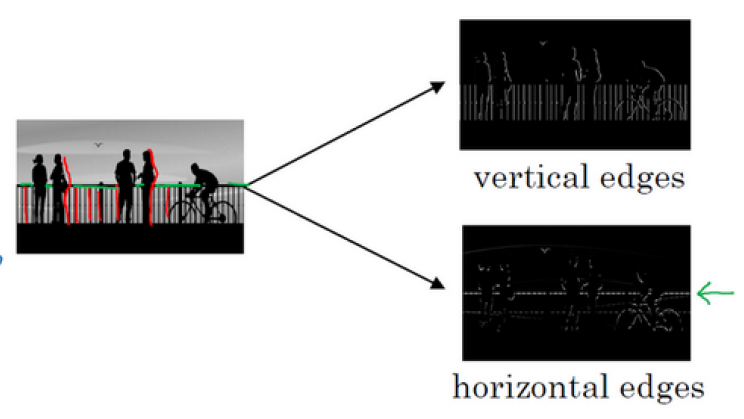
检测出这些边缘就需要用到 卷积运算

我们以垂直边缘检测为例，假设有一张 6 * 6 * 1 的灰度图像
我们需要像下面这样做卷积计算

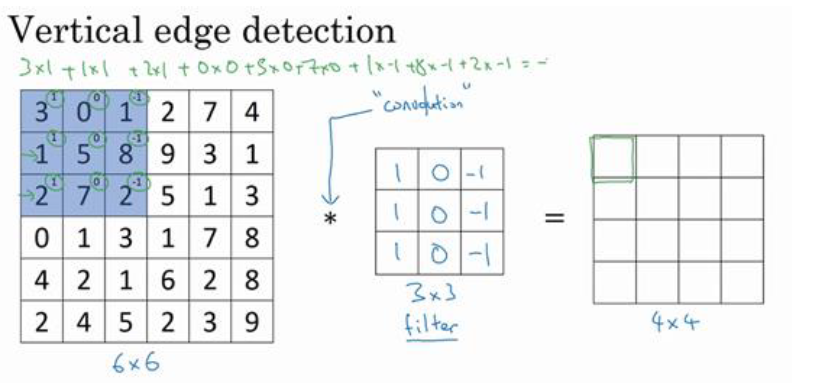
注意:

1. 中间的星号是数学中的卷积运算符，而不是python中的元素乘法。
2. 当前构造了一个3 * 3 的矩阵，被称为过滤器， 也有时被称为 核 (kernal)
3. 在数学中进行卷积计算时，一般先把过滤器进行镜像对称，但是在神经网络中我们不这么做（其实我们现在的计算方法在数学中叫做互相关）

为什么这个可以做垂直边缘检测呢？让我们来看另外一个例子。

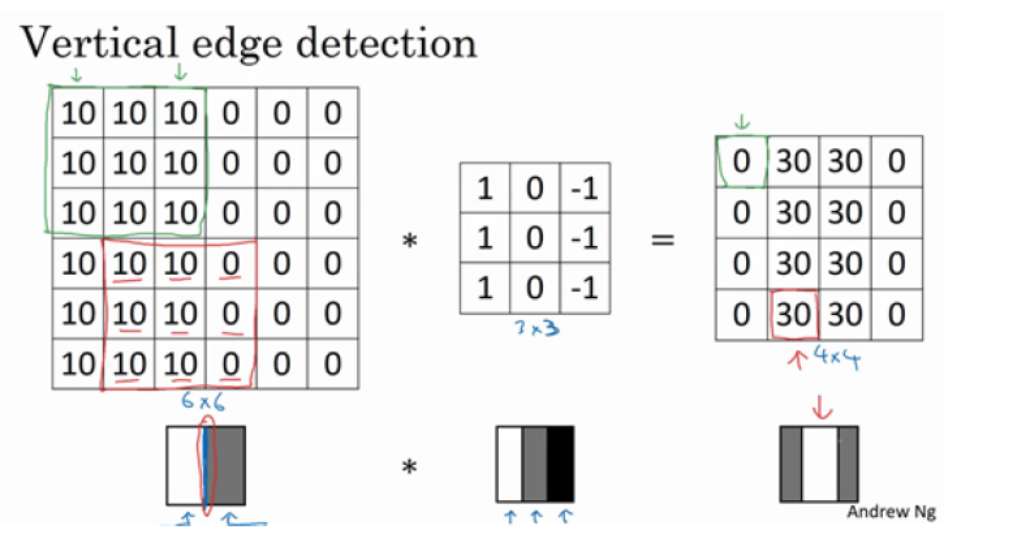
最后的图中有一个特别明显的垂直边缘线，目前之所以有点太宽了，是因为图片太小了。图片大了就正常了
如果不在乎中间是明线还是暗线，可以取绝对值

我们刚刚看了垂直边缘检测的过滤器，同理也可以知道水平边缘检测的过滤器

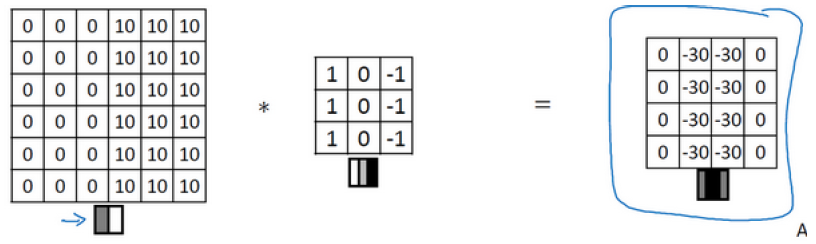
再看一个复杂一点的例子：

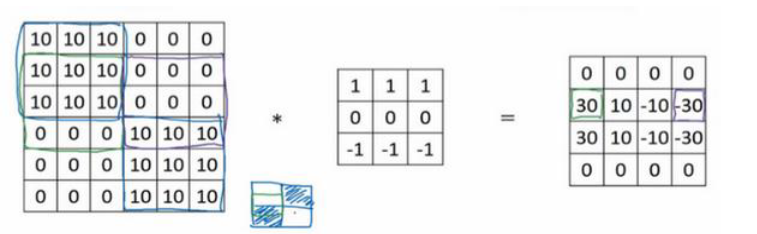
由于我们的图片尺寸太小，所以会有10和-10的过渡带，图片大一点就不会了

除了使用 1,0,-1 之外，其实还有一些数字选择

$$\text{Sobel filter matrix:} \begin{bmatrix} 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \end{bmatrix}$$ $$\text{Scharr filter matrix:} \begin{bmatrix} 3 & 0 & -3 \\ 10 & 0 & -10 \\ 3 & 0 & -3 \end{bmatrix}$$

这些筛选器有时可以提升鲁棒性，
现在甚至可以把这9个数字设置为9个参数，并使用反向传播算法来更新他们
这种过滤器对于数据的捕捉能力甚至可以胜过任何之前这些手写 的过滤器。
相比这种单纯的垂直边缘和水平边缘，它可以检测出45°或 70°，甚至是任何角度的边缘
我们会在迟一点学到这种过滤器

（二）Padding

假设图像尺寸 n * n , 过滤器尺寸 f * f， 那么输出的维度就是 (n- f +1) * (n- f +1)

这里有2 个问题：

1. 每次做卷积原图片都会变小
2. 图像中间的像素点被卷积计算了好几次，但是图像边缘的像素点没有被计算那么多次 。所以可能导致边缘的特征没有被捕捉到

因此，解决办法是在卷积操作前填充图像，比如在 6 * 6 的外边包裹一层像素， 变成 8 * 8
再用 3 * 3 的过滤器来卷积，就仍然得到 6 * 6

习惯上，可以用0来填充
如果填充的层数是 p , 输出就变成了 (n- f +2p +1) * (n- f +2p +1)

刚刚我们提到的是 p=1 的情况，至于填充多少像素，通常有两个选择：

1. Valid卷积： p=0， 不填充
2. Same卷积： p=(f-1)/2 卷积后图片大小不变 (一般把 f 设置为奇数)

（三）卷积步长

（Strided Convolutions）

目前我们都是一次移动1格， 但是如果把 步长 s 设置为2， 过滤器一次会跳过两个格子

此时输出尺寸变为：$\lfloor (\frac{n+2p-f}{s}+1) \rfloor \times \lfloor (\frac{n+2p-f}{s}+1) \rfloor$

其中 $\lfloor$ $\rfloor$ 是向下取整,
这意味着只在蓝框完全包括在图像或填充完的图像内部时，才对它进行运算。如果有任意一个蓝框移动到了外面，那就不要进行相乘操作。

（四）三维卷积

我们刚刚讲的都是灰度图像，那么对于RGB图像 比如 6 * 6 * 3， 该如何卷积呢？

你可以把它想象成 3 张 6 * 6 的图像的堆叠。现在我们不是把它和原来的 3 * 3 的过滤器做卷积，而是一个 3 * 3 * 3 的三维过滤器

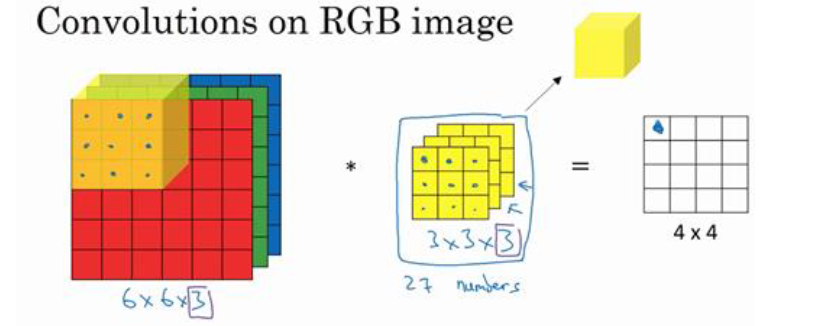
现在第一个6代表图像宽度，第二个6代表图像宽度，3 代表通道数目。图像的通道数必须和过滤器的通道数匹配

如果指向检测红色通道的边缘，可以将第一个过滤器设置为：

$$\begin{bmatrix} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \end{bmatrix}$$

剩下的绿色通道和蓝色通道的过滤器都设置为0
那么这个就是一个检测垂直边界的过滤器，但是只对红色通道有用
或者如果你不关心垂直边界在哪个颜色通道里，那就把 绿色通道和蓝色通道的过滤器 都设置成和 红色通道 一样就好了

如果不仅仅想要检测垂直边缘，而是要同时检测垂直边缘和水平边缘，甚至还有 45°倾斜的边缘，那么可以使用多个过滤器

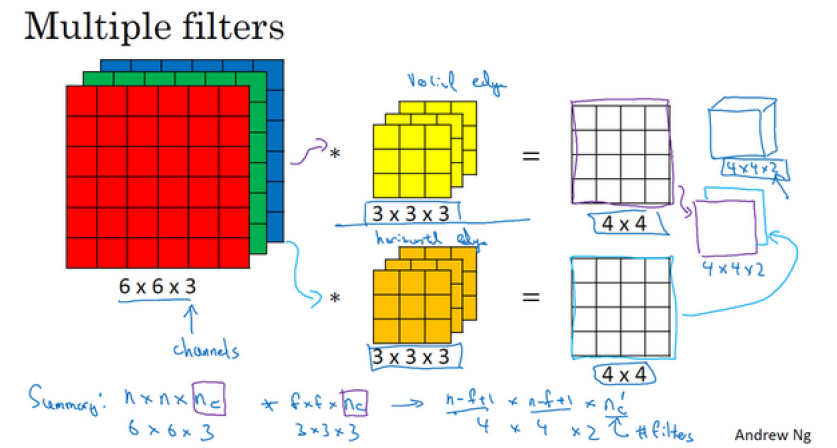
把两个输出按顺序堆叠，就得到了一个 4 * 4 * 2 的输出立方体， 这里的 2 来自于使用了几个不同的过滤器

总结一下， 如果输入图像为 $n \times n \times n_c$ ，其中 $n_c$ 是通道数目
然后卷积上 $n_{c^{'}}$ 个 $f \times f \times n_c$ 的过滤器，最后得到的输出就是：

$\lfloor (\frac{n+2p-f}{s}+1) \rfloor \times \lfloor (\frac{n+2p-f}{s}+1) \rfloor \times n_{c^{'}}$

$n_{c^{'}}$ 是过滤器的个数，也是下一层的通道数

（五）池化层

（Pooling Layers）

除了卷积层之外，池化层也可以减小图片的大小，提高计算速度，同时提高所提取特征的鲁棒性

我们一般采用的池化方法是 最大池化(Max pooling) ， 也就是取一个特定区域内的最大值

在下图中我们使用了 2 * 2 区域， 步长为 2 。 即 f=2 ， s =2

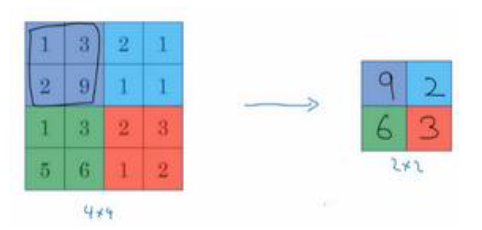
之前讲的计算卷积层输出大小的公式同样适用于最大池化，即： $\lfloor (\frac{n+2p-f}{s}+1) \rfloor \times \lfloor (\frac{n+2p-f}{s}+1) \rfloor \times n_c$

如果输入是三维的，输出也是三维的，通道数不变，宽高公式如上

池化层的原理：数字大意味着可能探测到了某些特定的特征。它会保留在最大化的池化输出里。

注意：

1. 池化层有一组超参数，但并没有参数需要学习。一旦确定了 𝑓和 𝑠，它就是一个固定运算，梯度下降无需改变任何值。
   因此有时候池化层不被作为一个层，或者和一个卷积层一起作为一个层
2. 还有一种池化叫平均池化，不太常用
3. 大部分情况下，最大池化很少用padding

（六）卷积神经网络

我们先来看单层卷积神经网络

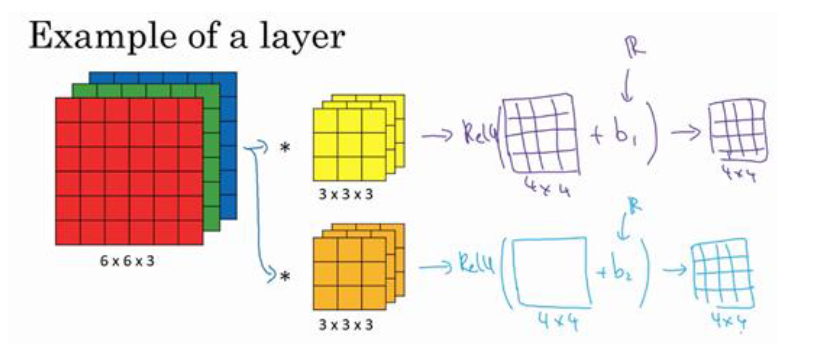
我们之前讲过：

$$Z^{[l]} = W^{[l]} X + b^{[l]}\\ A^{[l]} = g^{[l]}(Z^{[l]})$$

这里的过滤器都可以用 $W^{[l]}$ 来表示，激活函数可以使用 Relu
记得在激活函数前还有加上偏差b，用python广播机制实现
注意，无论输入的图片有多大，需要更新的参数都是取决于过滤器，即 $n_{c^{'}} \times f \times f \times n_c$
$n_{c^{'}}$ 就是过滤器的数量，也是提取的特征数

总结一下尺寸:

输入尺寸：$n_H^{[l-1]} \times n_W^{[l-1]} \times n_c^{[l-1]}$

输出尺寸：$n_H^{[l]} \times n_W^{[l]} \times n_c^{[l]}$

筛选器尺寸：$f^{[l]} \times f^{[l]} \times n_c^{[l-1]}$

Weights(多个筛选器)： $f^{[l]} \times f^{[l]} \times n_c^{[l-1]} \times n_c^{[l]}$

偏差bias： $1 \times 1 \times 1 \times n_c^{[l]}$

$A^{[l]}$ : $m \times n_H^{[l]} \times n_W^{[l]} \times n_c^{[l]}$

其中 ：
$n_H^{[l]} = \lfloor \frac{n_H^{[l-1]}+2p^{[l]}-f^{[1]}}{s^{[l]}}+1 \rfloor$ $n_W^{[l]} = \lfloor \frac{n_W^{[l-1]}+2p^{[l]}-f^{[1]}}{s^{[l]}}+1 \rfloor$

现在我们已经知道了如何为卷积神经网络构建一个卷积层，那如何构建一个深度卷积神经网络呢？

如下图所示,假设要识别输入的 39 * 39 * 3 的图像里有没有猫，每一层都使用了 valid卷积，也就是padding为0
第一层用了 10 个过滤器，第二层用了 20个过滤器，第三层用了 40 个过滤器
具体参数见图中

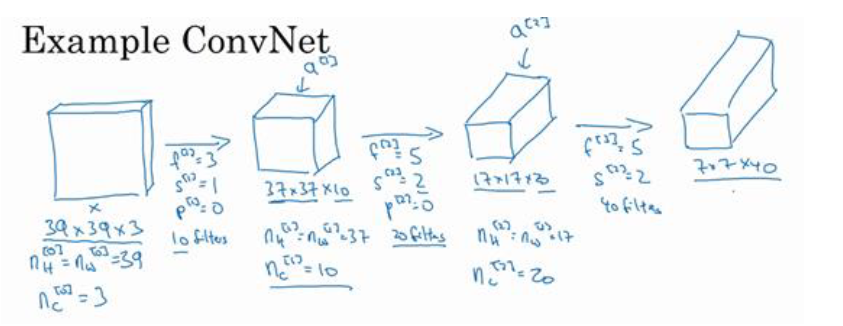
到此这张39 * 39 * 3 的图像处理完毕了，最后提取了 7 * 7 * 40 个特征
然后对该卷积进行处理，可以将其平滑或展开成 1960个单元，输出为一个向量，
其填充内容是logistic回归单元还是 softmax回归单元取决于我们是想识图片上有没有猫，还是想识别 𝐾 种不同类型中的一个

举个例子：假设要分为10种类型，那应该怎么处理最后一个卷积层 7 * 7 * 40 的输出？

1. 将最后一个卷积层的输出，即 7 * 7 * 40 的三维特征图（feature map），展开 成一个一维的长为1960的向量。
2. 在 Softmax 层， 将 1960 * 1 的矩阵 使用一个全连接层 转化成 10 * 1 的向量。 W的尺寸是 10 * 1960，

$$z_i^{[1]} = w_i^{[1]T} x + b_i^{[1]}$$

3. 在 Softmax 层，对于每个类别 k，你将计算该类别的得分的指数与所有类别得分的指数和的比例。公式如下：

$$a_i^{[l]}=\frac{e^{z_i^{[1]}}}{\sum_{j=1}^{10} e^{z_j^{[1]}}}$$

注意:

1. 随着神经网络加深。图片宽高应该变小，通道数应该变大
2. 一个典型的神经网络通常有 3 层， 。
3. 卷积层用CONV 来表示， 池化层用 POOL 来表示， 全连接层用FC 表示

现在我们要往卷积神经网络中加入池化层，该如何实现呢？

下面给出了一个例子，用于识别手写数字是 1 - 9，参考的参数来源是LeNet-5模型，但这里并不是LeNet-5模型

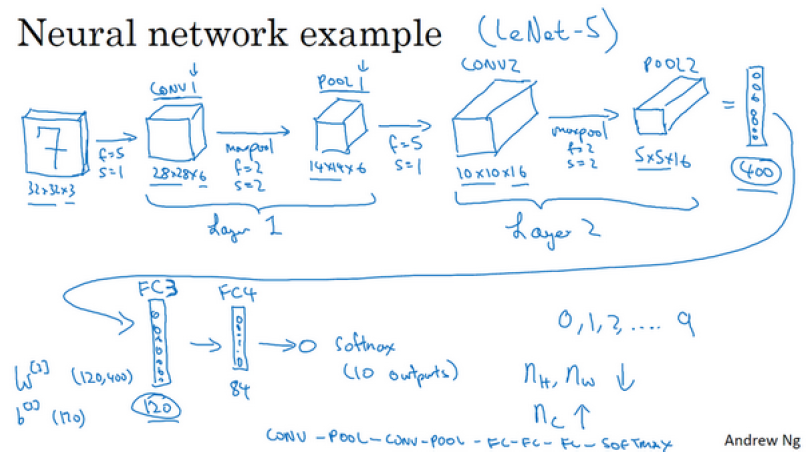
关于这个模型，我们有几点需要注意：

1. 第一层的过滤器 f =5, stride=1, 使用了6个过滤器，padding=0， 使用了ReLU函数，其它层类似如图
2. 由于池化层没有需要更新的参数，所以把一个池化层和一个卷积层合起来作为一个层
3. 全连接层 FC3 就是普通的神经网络，权重W尺寸为 120 * 400
4. 随着神经网络的深度不断加深，高度 $n_H$ 和 宽度 $n_W$ 通常会减少，通道数量会增加
5. 在神经网络中，另一种常见模式就是一个或多个卷积后面跟随一个池化层，然后再是一个或多个卷积层后面再跟一个池化层，然后是几个全连接层，最后是一个 softmax。
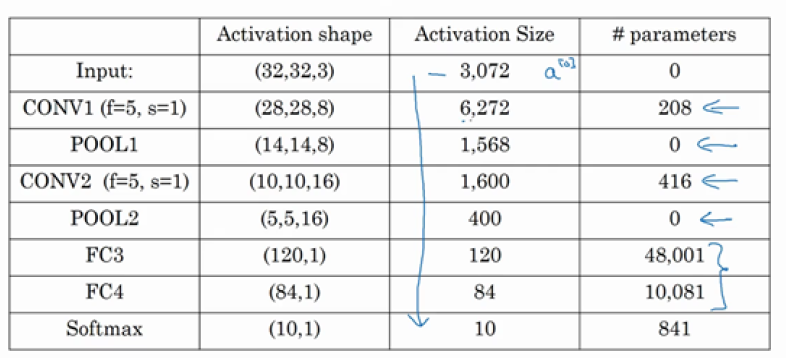
6. 参数的大小如下图，可以看见大部分参数在全连接层：

代码实现

典型 CNN 代码示例（手写数字识别 10 类）

结构总结

层次	操作	输出 shape
输入	32x32x1
Conv1	5x5, 6 filters	28x28x6
Pool1	2x2	14x14x6
Conv2	5x5, 16 filters	10x10x16
Pool2	2x2	5x5x16
Conv3	5x5, 120 filters	1x1x120
Flatten	-	120
FC1	120 → 84	84
FC2	84 → 10	10（softmax logits）

随着卷积层加深：

• 图像宽高 越来越小（下采样 Pooling）
• 通道数（feature map） 越来越多
• 最后拉平 → 全连接 → softmax 分类

import torch
import torch.nn as nn
import torch.nn.functional as F

class SimpleCNN(nn.Module):
    def __init__(self, num_classes=10):  # 10 类分类
        super(SimpleCNN, self).__init__()
        
        # 第1层: 卷积 + ReLU + 池化
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, stride=1, padding=0)
        self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2)
        
        # 第2层: 卷积 + ReLU + 池化
        self.conv2 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5, stride=1, padding=0)
        self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
        
        # 第3层: 卷积 + ReLU
        self.conv3 = nn.Conv2d(in_channels=16, out_channels=120, kernel_size=5, stride=1, padding=0)
        
        # 全连接层
        self.fc1 = nn.Linear(120, 84)
        self.fc2 = nn.Linear(84, num_classes)  # 输出 num_classes 维
        
    def forward(self, x):
        # 输入 x: (batch_size, 1, 32, 32) 假设输入是 32x32 灰度图
        
        x = self.conv1(x)          # (batch_size, 6, 28, 28)
        x = F.relu(x)
        x = self.pool1(x)          # (batch_size, 6, 14, 14)
        
        x = self.conv2(x)          # (batch_size, 16, 10, 10)
        x = F.relu(x)
        x = self.pool2(x)          # (batch_size, 16, 5, 5)
        
        x = self.conv3(x)          # (batch_size, 120, 1, 1)
        x = F.relu(x)
        
        # 展平为 (batch_size, 120)
        x = x.view(-1, 120)
        
        x = self.fc1(x)            # (batch_size, 84)
        x = F.relu(x)
        
        x = self.fc2(x)            # (batch_size, num_classes)
        
        return x

训练时配的 loss

model = SimpleCNN(num_classes=10).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
criterion = nn.CrossEntropyLoss()

训练循环

for epoch in range(num_epochs):
    model.train()
    for images, labels in train_loader:
        images = images.to(device)
        labels = labels.to(device)
        
        outputs = model(images)
        loss = criterion(outputs, labels)
        
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

（七）经典的神经网络

（1）LeNet-5 网络

LeNet-5 是 针对灰度图片训练的，所以图片的大小只有 32×32×1, 用于识别手写数字

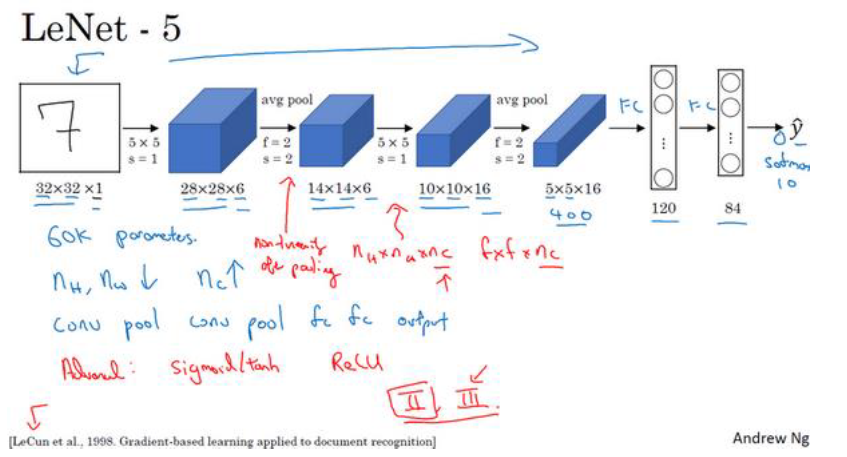
注意：

1. 在这篇论文写成的那个年代，人们更喜欢使用平均池化，而现在我们可能用最大池化更多一些。
2. 这个神经网络中还有一种模式至今仍然经常用到，就是一个或多个卷积层后面跟着一个池化层，然后又是若干个卷积层再接一个池化层，然后是全连接层，最后是 Softmax和输出

（2）AlexNet 网络

AlexNet 首先用一张 227×227×3的图片作为输入，实际上原文中使用的图像是 224×224×3 但是如果你尝试去推导一下，你会发现 227×227这个尺寸更好一些。

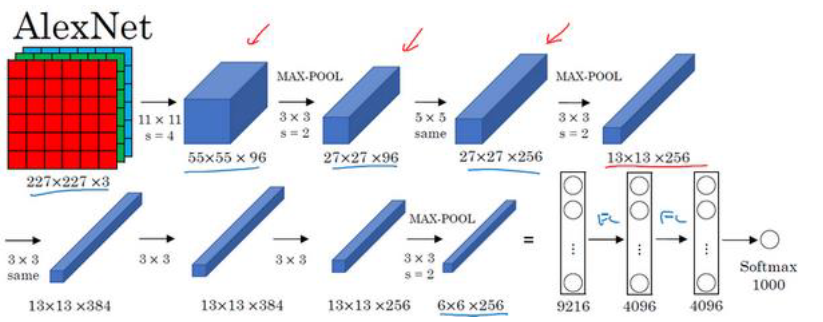
注意：

1. 实际上，这种神经网络与 LeNet 有很多相似之处，不过 AlexNet 要大得多。 LeNet-5大约有 6万个参数，而 AlexNet包含约 6000万个参数。
2. AlexNet 比 LeNet 表现更为出色的另一个原因是它使用了 ReLu 激活函数。
3. 第一点，在写这篇论文的时候， GPU的处理速度还比较慢，所以 AlexNet采用了非常复杂的方法在两个 GPU上进行训练。大致原理是，这些层分别拆分到两个不同的GPU上，同时还专门有一个方法用于两个 GPU进行交流。
4. 论文还提到，经典的 AlexNet 结构还有另 一种类型的层，叫作 “局部响应归一化层”，即 LRN层，这类层应用得并不多

（3）VGG-16

VGG-16网络没有那么多超参数，这是一种只需要专注于构建卷积层的简单网络。

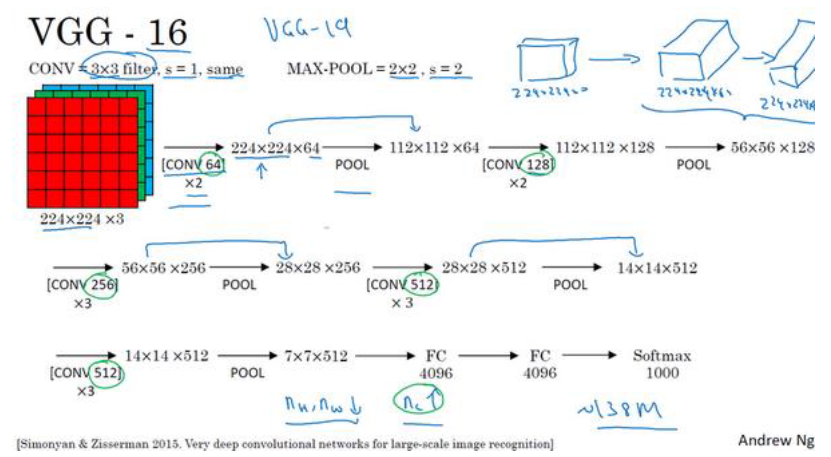
注意：

1. 这里采用的都是大小为 3×3 步幅为 1的过滤器，并且都是采用 same卷积
2. VGG-16的这个数字 16，就是指在这个网络中包含 16个卷积层和全连接层。共包含约 1.38亿个参数，即便以现在的标准来看都算是非常大

（八） 1×1 卷积

当卷积层的过滤器尺寸为1 * 1 时，另有妙用

如果某一层的图片输出已经是 6 * 6 * 32 ，对他进行 1 * 1 卷积所实现的功能就是遍历这 36 个单元格，
计算每个单元格的32个数字之和，然后使用ReLU激活

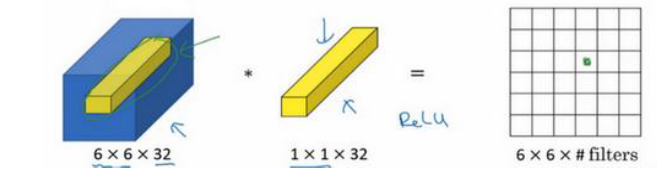
这种方法通常 称为 1×1卷积，有时也被称为 Network in Network
这个方法可以在不改变宽高的情况下，用于压缩通道数 或者 自由地控制通道数
而相反池化层则是压缩宽高，不改变通道数