第 6 课：超参数调试，Batch正则化，Softmax回归

（一）如何选择最合适的超参数

我们已经知道很多的超参数了，但是这些超参数的重要性是不同的。
优先级大到小排列如下:

1. 学习率 $\alpha$
2. 动量梯度下降算法的 $\beta$, 隐藏层单元，mini-batch size
3. 层数，学习率衰减率 > Adam 算法的 $\beta_1,\beta_2,\epsilon$

那如何测试出最好的超参数呢?

对于一组超参数而言，如下图所示，当我们测试的次数有限时，建议采用右边的取点方法。

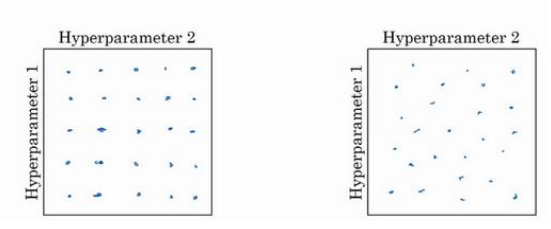
因为左图中每个参数只采用了5个值，而右图中每个参数尝试了25个值，所以可以更好地观察哪个参数更重要
拓展到3个参数的组合尝试中也是如此

在所有的采样点中测试出最好的之后，可以选择进一步精细化测试

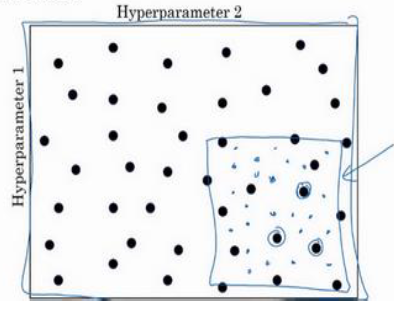
此外，对于单个参数在一定范围内的取点测试，不建议均匀分布随机取点
举个例子，如果某个参数要从50试到100，那么我们可以均匀取样
但是如果某个参数要从0.0001 试到 1， 那么最好像 0.0001， 0.001 ，0.01， 0.1， 1 这样取样（但仍需是随机取样）
在python中可以这样实现:

r = -4* np.random.rand()  # r 属于[-4,0]
a = 10**r               # a 属于[10-4,1]

那么对于像 $\beta$ 这样的0.9 到0.999之间取样的该如何实现呢？

r = -2* np.random.rand()-1  # r 属于[-3,-1]
beta = 1-10**r            # beta 属于[0.999,0.9]

为什么要这样取点呢？因为在深度学习中，很多时候在某个范围内参数的影响力会突然变大很多
比如在 $\beta$ 靠近1时，所代表的平均天数 1/(1-$\beta$) 会变大得非常迅速，所以要在这个范围内尝试更多的点

然而，我们上面讨论的都是给定参数后，完整地测试一次之后对各组的测试结果进行比较
但是如果进行一次实验的成本非常高，时间非常长，我们只能做一两次实验，该怎么确定最优参数呢？

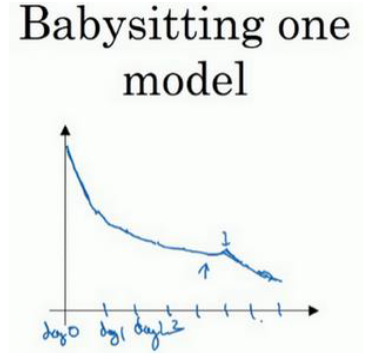
如下图，我们可以采用这种 Babysitting one Model
也就是在指定的时间间隔内调整一次参数，观察输出的成本函数的变化

（二）Batch归一化

（Batch Normalizing）

我们之前讲过归一化输入来把原始数据X 的均值降到 0， 方差缩放到1·：

$$X_{\text{std}} = \frac{X - \mu}{\sigma}$$

其中 $\mu$ 是特征的均值，$\sigma$ 是特征的标准差。

$$\mu = \frac{1}{m} \sum_{i=1}^m x_i$$ $$\sigma = \sqrt{\frac{1}{m} \sum_{i=1}^m (x_i - \mu)^2}$$

我们知道这种方法把扁平的数据拉伸得饱满，可以加快学习过程

那么同理可得，既然可以把输入样本 X 进行归一化，是不是可以把每一层的输出 a 都归一化呢？
事实上这是可以的，但是我们一般归一化的是 $z^{[l]}$ 而不是 $a^{[l]}$， 归一化可以使下一层的 w 和 b 训练得更快

假设第 l 层有 m 个隐藏节点，其中 $\mu$ 是特征的均值，$\sigma$ 是特征的标准差。

$$\mu = \frac{1}{m} \sum_{i=1}^m Z^{[l](i)}$$ $$\sigma^2 = \frac{1}{m} \sum_{i=1}^m (Z^{[l](i)} - \mu)^2$$ $$Z_{norm}^{[l](i)} = \frac{Z^{[l](i)} - \mu}{\sqrt{\sigma^2+\epsilon}}$$

注： $\epsilon$ 用于防止分母为0

现在的每个隐藏单元都含有平均值0和方差1，但是也许隐藏单元有了不同的分布会有意义，所以我们手动修改其平均值和方差

$$\tilde{Z}^{[l](i)} = \gamma*Z_{norm}^{[l](i)} + \beta,$$

这样我们就可以随意修改 $Z^{[l](i)}$ 的平均值

在神经网络中，我们不再使用 $A^{[l]}= g^{[l]}(Z^{[l](i)})$, 而是 $A^{[l]}= g^{[l]}(\tilde{Z}^{[l](i)})$

注意:

1. 在过程中我们引入了新的参数 $\gamma^{[l]} ， \beta^{[l]}$，这对于每层是不一样的

2. 这里的 $\beta$ 和 指数加权平均数（比如Adam算法等）中的 $\beta$ 不是一个东西，这里的是用于正则化控制平均值的

3. $\gamma^{[l]} ， \beta^{[l]}$ 并不是超参数！这是需要更新的参数，和W跟b一样！
   我们可以使用任意的优化算法，可以是 Adam、RMSprop、Momemtum, 或者只是普通的梯度下降
   然后更新参数,例如：

   $$\beta^{[l]} = \beta^{[l]} - \alpha* d\beta^{[l]}$$

4. 实践中，Batch归一化通常和 mini-batch一起使用,每一个mini-batch $X^{{1}}$ 中的计算方法都和上面相同

5. 事实上，由于在Batch归一化的过程中首先把平均值拉到了0，所以实际上 $b^{[l]}$ 被约掉了。可以暂时把它设置为0

6. $Z^{[l]}$ 的维数是 $(n^{[l]},1)$
   $b^{[l]}$ 的维数是 $(n^{[l]},1)$
   $\beta^{[l]}$ 的维数是 $(n^{[l]},1)$
   $\gamma^{[l]}$ 的维数是 $(n^{[l]},1)$

Batch 归一化的优点：

除了我们之前说过的，归一化可以把扁平的数据变得饱满从而加速计算之外，Batch归一化还有其他优点：

1. 减轻 internal covariate shift（减少层之间耦合）

   稳定每层的输入，权重更新不再依赖于前一层特定的权重分布，因此，每一层都可以在相对独立的环境中学习和适应。

2. 提高深层网络训练稳定性 确保每层的输入保持相同的分布，它减少了层与层之间参数更新的相互依赖性。
   这意味着即使前面层的参数发生了变化，也不会极大地影响到后面层的学习进程。

3. 加速收敛
   这种特性使得每一层都能在更加独立的环境中进行学习，降低了层间复杂的相互作用，有助于网络更快地收敛。

4. 对于输入分布变化更鲁棒

   即使训练数据在某些方面不够代表性（如只有黑猫），Batch归一化也有助于模型在面对不同类型（如有色猫）的数据时，保持稳定的性能。因为Batch归一化减少了模型对输入数据具体特征的敏感度，使得模型对于输入数据中的细微变化更加鲁棒。

5. 有轻微正则化效果（类似 Dropout）

   在每个 mini-batch 中计算均值和方差，而不是在整个数据集上，用一小部分的数据计算导致了每个隐藏层上都有噪音
   和 dropout 类似，这样迫使后部单元不过分依赖任何一个隐藏单元，但是效果比较轻微
   因此单个 mini-bacth 越大，Batch归一化的正则化效果越弱

Batch 归一化的缺点

1. 训练时必须用 minibatch，batch_size 太小时效果差
2. 对 RNN 不适用（变长序列不方便 BN，RNN 更常用 LayerNorm）
3. 小 batch_size 时估计均值方差不准，导致训练不稳定
4. 推理时需要保存 moving average 均值、方差

Batch 归一化的测试过程

我们现在已经知道了如何在训练过程中使用Batch归一化，但是放到测试时，该怎么做呢？
我们现在对于单个mini-batch中的某个隐藏层的计算方法如下，其中 m 是这个mini-batch中的样本数量，而不是整个训练集

$$\mu = \frac{1}{m} \sum_{i=1}^m Z^{[l](i)} \\ \sigma^2 = \frac{1}{m} \sum_{i=1}^m (Z^{[l](i)} - \mu)^2 \\ Z_{norm}^{[l](i)} = \frac{Z^{[l](i)} - \mu}{\sqrt{\sigma^2+\epsilon}} \\ \tilde{Z}^{[l](i)} = \gamma*Z_{norm}^{[l](i)} + \beta,$$

但是问题是，在测试时，我们是逐个测试样本的，而不是把一个 mini-batch 中的所有样本同时处理
而单个样本的 $均值\mu, 方差\sigma^2$ 没有意义，因此需要单独估算 $\mu, \sigma^2$， 这可以使用指数加权平均数来实现

对不同的mini-batch $X^{\{1\}},X^{\{2\}},X^{\{3\}},……$ 的第l层训练时，我们得到了$\mu^{\{1\}[l]},\mu^{\{2\}[l]},\mu^{\{3\}[l]},……$
然后对这些值进行指数加权平均就可以得到最后测试集所需要的 $\mu$ 了， $\sigma^2$ 也是同理

最后在测试时，也要进行对应的batch归一化，用的就是测试集的 Z 和 用指数加权平均数 估算出来的 $\mu$ 和 $\sigma^2$

但是在使用 Pytorch 过程中，并没有这个问题

代码实现

Batch Normalization（BN） 属于 步骤 3：模型结构（Model/Network）

• 对 全连接层，用 nn.BatchNorm1d
• 对 卷积层，用 nn.BatchNorm2d

import torch.nn as nn

class MLP(nn.Module):
    def __init__(self):
        super(MLP, self).__init__()
        self.fc1 = nn.Linear(784, 256)
        self.bn1 = nn.BatchNorm1d(256)  # BatchNorm
        self.relu1 = nn.ReLU()
        
        self.fc2 = nn.Linear(256, 128)
        self.bn2 = nn.BatchNorm1d(128)
        self.relu2 = nn.ReLU()
        
        self.fc3 = nn.Linear(128, 1)
        self.sigmoid = nn.Sigmoid()
        
    def forward(self, x):
        x = self.fc1(x)
        x = self.bn1(x)
        x = self.relu1(x)
        
        x = self.fc2(x)
        x = self.bn2(x)
        x = self.relu2(x)
        
        x = self.fc3(x)
        x = self.sigmoid(x)
        
        return x

卷积神经网络 CNN 示例

nn.Conv2d(in_channels, out_channels, kernel_size)
nn.BatchNorm2d(out_channels)

（三）Softmax回归

我们之前学的都是二分类，但是如果要实现多分类，就要用到 Softmax 回归层，使得最后输出的结果是一个数组。
假设我们要识别猫、狗和鸡， 那么这个输出数组可以是 [ 0.1 , 0.5 , 0.4 ] ,这样显而易见狗的概率最大。
同时要确保数组中的所有概率之和为 1

之所以叫 Softmax， 是因为形如 [0, 1, 0] 这样的只有一个1的全零数组叫 Hardmax

我们用 C 来表示类别个数，Softmax 层的计算方法如下：

$$z_i^{[1]} = w_i^{[1]T} x + b_i^{[1]}$$ $$a_i^{[l]}=\frac{e^{z_i^{[1]}}}{\sum_{j=1}^C e^{z_j^{[1]}}}$$

注意:
Z 应该是一个 4 * 1 的数组

我们可以把上面的第二步当做 Softmax 的激活函数

$A^{[l]}=g^{[l]}(Z^{[l]})$

这一激活函数的特殊之处在于，这个激活函数 𝑔 需要输入一个 4×1维向量，然后输出一个 4×1维向量
而之前，我们的激活函数都是接受单行数值输入，例如 Sigmoid 和 ReLu 激活函数，输入一个 实数，输出一个实数。

在图像上，可以这么理解

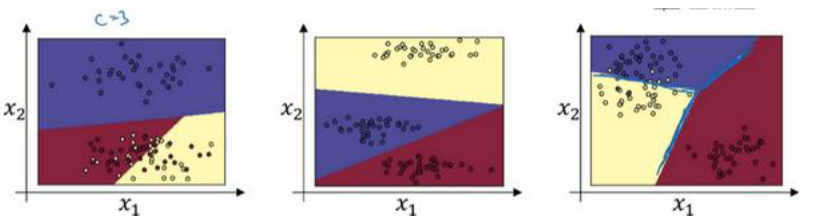
我们可以发现，任何两个分类之间的决策边界都是线性的

注意：

1. Softmax 通常被用作神经网络的最后一层。
   它的作用是将网络的原始输出，即 logits 转换成概率分布，这有助于直接从输出层解读每个类别的预测概率
2. 如何知道输出数组中的每个值代表哪个类别？
   在训练神经网络时，你需要预先定义类别的顺序，并在整个模型训练和预测过程中保持这一顺序不变。

Softmax的损失函数

由于现在最后 的输出不是单个值，而是一个数组，所以损失函数也要重新定义
在 Softmax 分类中，一般用的损失函数是：

$$L(\hat{y}, y) = -\sum_{j=1}^{4} y_j \log \hat{y}_j$$

举个例子：

$$y=[0, 1, 0, 0] \\ \hat{y} = [0.3, 0.2, 0.1, 0.4]$$

在这种情况下，想要让损失函数尽可能小，就必须让 $\hat{y}_2$ 尽可能大，也就是尽可能准确

上面是单个样本的损失函数，整个训练集的成本函数定义如下：

$$J(w^{[1]}, b^{[1]}, \ldots) = \frac{1}{m} \sum_{i=1}^{m} L(\hat{y}^{(i)}, y^{(i)})$$

关于向量化时的数据尺寸如下

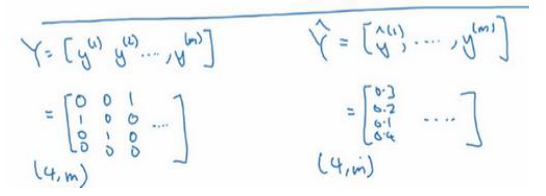
如果 C=4，那么 $y^{(1)},y^{(2)},…… , y^{(m)}$ 都是 4 × 1 的向量， 而 Y 最终是一个 4 * m 的矩阵，同样的 $\hat{Y}$ 也是一个 4 * m 的矩阵

最后我们来看一下，在有 Softmax 输出层时如何实现梯度下降法:
输出层的尺寸是 C * 1
计算方法如下：

$$dZ^{[l]} = \hat{y}-y$$

现在看起来 Softmax 可能有点抽象，但是我们会在下面的卷积神经网络中用具体的图像识别例子来理解

代码实现

Softmax 属于 步骤 3：模型结构（Model/Network）

• Softmax 是 激活函数，属于模型最后一层的设计
• 用来 把 logits（未归一化分数）转成概率分布
• 多分类问题通常使用 Softmax 作为输出层
• 损失函数搭配用 CrossEntropyLoss （自动包含 Softmax + log）

直接写 Softmax + NLLLoss

import torch.nn as nn

model = nn.Sequential(
    nn.Linear(784, 128),
    nn.ReLU(),
    nn.Linear(128, 4),          # C=4 类别
    nn.Softmax(dim=1)           # Softmax 激活
)

criterion = nn.NLLLoss()

更常用写法 → 不用 Softmax，直接用 CrossEntropyLoss

CrossEntropyLoss = log(Softmax) + NLLLoss

model = nn.Sequential(
    nn.Linear(784, 128),
    nn.ReLU(),
    nn.Linear(128, 4)           # 输出 logits，不加 Softmax
)

criterion = nn.CrossEntropyLoss()

训练时：

outputs = model(images)        # shape: (batch_size, 4)
loss = criterion(outputs, labels)  # labels = (batch_size), 值为 0~3

完整示例

import torch.nn as nn

class MLP(nn.Module):
    def __init__(self, num_classes=4):
        super(MLP, self).__init__()
        self.fc1 = nn.Linear(784, 128)
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(128, num_classes)  # 输出 logits，C 类别

    def forward(self, x):
        x = self.fc1(x)
        x = self.relu(x)
        x = self.fc2(x)  # logits
        return x

model = MLP(num_classes=4)
criterion = nn.CrossEntropyLoss()