第 5 课：算法的优化

（一）Mini-batch 梯度下降

（Mini-batch gradient descent）

mini-batch 算法的过程

我们之前尝试过，对于大量的训练数据，进行一次梯度下降的时间非常长。

$X = [x^{(1)}, x^{(2)}, \dots, x^{(m)}]$ 。 维度 $n_x \times m$

$Y = [y^{(1)}, y^{(2)}, \dots, y^{(m)}]$ 。 维度 $1 \times m$

现在把 X 分为很多个小集合，称为mini-batch。

比如把 $x^{(1)}到 x^{(100)}$ 作为一个mini-batch， 称为 $X^{\{1\}}$,

那么如果 $X = [x^{(1)}, x^{(2)}, \dots, x^{(1000)}]$，则就可以拆分为$X^{\{1\}}$ 到 $X^{\{10\}}$

同理，如果 $Y = [y^{(1)}, y^{(2)}, \dots, y^{(1000)}]$，则就可以拆分为$Y^{\{1\}}$ 到 $Y^{\{10\}}$

所以 $X^{\{t\}}$ 的大小为 $n_x \times n$ , $Y^{\{t\}}$ 的大小为 $1 \times n$，其中 n 为单个 mini-batch 的样本数

注意：

使用小括号上标表示第几个训练样本， 中括号上标表示第几层，大括号上标表示第几个 mini-batch

之前我们有

$$Z^{[l]} = W^{[l]} X + b^{[l]}\\ A^{[l]} = g^{[l]}(Z^{[l]})$$

现在对于每一个mini-batch就会改为

$$Z^{[l]} = W^{[l]} X^{\{t\}} + b^{[l]} \\ A^{[l]\{t\}} = g^{[l]}(Z^{[l]})$$

对应的成本函数改为

$$J(w, b) = \frac{1}{m} \sum_{i=1}^m L(\hat{y}^{(i)}, y^{(i)})$$

其中：

1. m是单个minibatch中的样本数
2. $L(\hat{y}^{(i)}, y^{(i)})$ 是一个mini-batch $X^{\{t\}},Y^{\{t\}}$ 中的样本

如果使用正则化，则

$$J^{\{t\}} = \frac{1}{l} \sum_{i=1}^{l} L(\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2l} \sum_{l} \lVert w^{[l]} \rVert_F^2,$$

反向传播也是同理。

我们可以发现对于单个mini-batch，计算步骤和之前普通的batch梯度下降算法是完全相同的。

对于每一个 mini-batch , 都要进行一轮完整的正向和反向传播，计算损失函数，并且更新权重

所以使用batch梯度下降算法一次只能梯度下降一次，但是使用mini-batch梯度下降算法每个mini-batch都可以梯度下降一次

同时，一次遍历所有mini-batch，也就是遍历整个X，称为一个 迭代（epoch）

注意：

样本小于2000个时，不使用mini-batch，

样本数量较大时，把一个 mini-batch 的大小设置为64、128、256 或 512 （2的指数）

mini-batch 算法的原理

在使用batch算法时，成本函数应该是单调递减的，除非学习率过大

但是对于 mini-batch 而言，应该如下图,因为每次下降用的都是不同的训练集

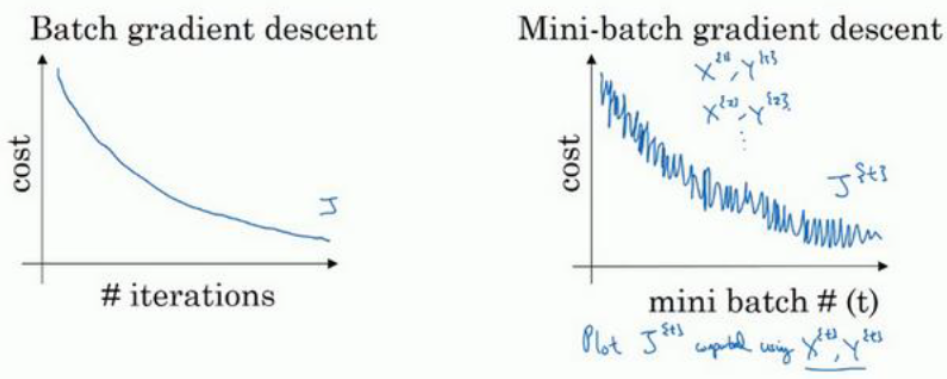
而更形象地表现如下

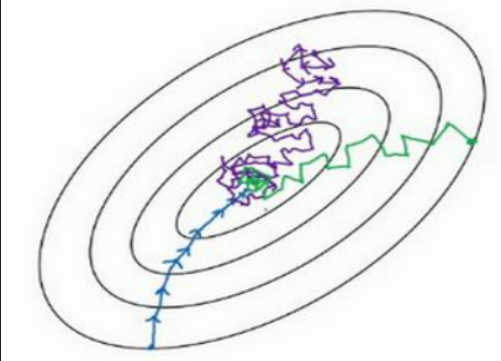
其中:

• 蓝线是batch梯度下降算法，也就是把一个mini-batch 的大小设置为 m

• 紫线是随机梯度下降算法（SGD），也就是把一个mini-batch 的大小设置为 1

• 绿线是mini-batch梯度下降算法，也就是把一个mini-batch 的大小设置为 1000

这种算法仍然存在如下弊端：

1. 折线摆动靠近最优解，太慢
2. 学习率不能太大，不然不能在最优解附近收敛

代码实现

我们继续按照 PyTorch 五大步骤 定位：minibatch 属于：步骤 2：数据加载与预处理（DataLoader）

• minibatch 本质上是“如何把大数据集切分成小块”
• PyTorch 用 torch.utils.data.DataLoader 实现自动 batch 切分

from torch.utils.data import DataLoader

train_loader = DataLoader(train_dataset, batch_size=128, shuffle=True, num_workers=4)

test_loader = DataLoader(val_dataset, batch_size=128, shuffle=False, num_workers=4)

参数	含义
batch_size	minibatch 大小（常用 64、128、256、512）
shuffle	每个 epoch 是否打乱样本顺序（训练集要 shuffle）
num_workers	多进程读取数据，加快 IO

在训练循环中体现

for images, labels in train_loader:
    # 每次循环是一个 minibatch
    # images.shape → (batch_size, ...)
    # labels.shape → (batch_size, ...)
    
    outputs = model(images)
    loss = criterion(outputs, labels)
    
    loss.backward()
    optimizer.step()

（二）动量梯度下降算法

（Gradient descent with Momentum）

在了解这种算法之前，我们需要先学习一下指数加权平均数

（1）指数加权平均数

（Exponentially weighted averages）

这是一种便捷地得到动态拟合曲线的方法

$$v_0=0 \\ v_1=0.9v_0+0.1\theta_1 \\ v_2=0.9v_1+0.1\theta_2 \\ v_3=0.9v_2+0.1\theta_3 \\ \dots \\ v_t=0.9v_{t-1}+0.1\theta_t \\$$

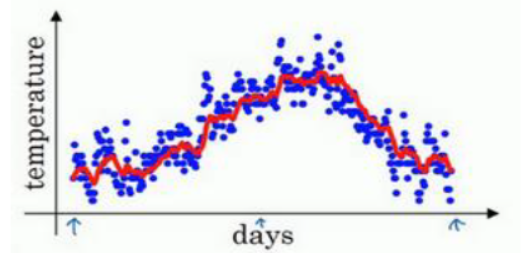
其中： $v_t$ 是某一天的加权平均数，$\theta_t$ 是某一天的值

就可以得到关于 $v_t$ 和 t 的关系图

公式如下：

$$v_0=0 \\ v_t=\beta v_{t-1}+(1-\beta)\theta_t \\ \\ 此时 v_t 可以视为是 \frac{1}{1-\beta} 天的平均值$$

显而易见, $\beta$ 越趋近于1， 曲线越平缓，对于变化适应的更慢

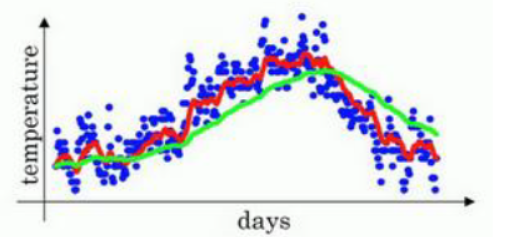
由于一开始 $v_0=0$， 所以曲线一开始应该是从0开始的，因此前几天的值拟合的不好

所以可以选择使用 指数加权平均的偏差修正 (Bias correction in exponentially weighted averages)

公式修改成如下:

$$v_t=\frac {\beta v_{t-1}+(1-\beta)\theta_t}{1-\beta^t} \\$$

注意:

1. 在实际代码中，一般不把 $v_1, v_2$ 之类变量分开，而是不断地更新v

   v=beta*v+(1-beta)*theta
   

2. 偏差修正不是必须的，因为除了开头的几个样本，后面的几乎没有区别。甚至一般不怎么用
3. 动量梯度下降算法其实跟动量没有关系，使用动量Momentum只是一种比喻。
   其实用惯性更好理解。动量大的物体更难以轻易改变运动状态，对应到算法中就是更平滑，更难以产生摆动

（2）动量梯度下降算法

无论是batch梯度下降 还是mini-batch梯度下降 ，在每次反向传播的时候都需要计算 $dW^{l},db^{l}$，并且用他们来更新 $W^{l},b^{l}$

但是这个算法不直接使用 $dW^{l},db^{l}$， 而是使用他们的 指数加权平均数 来更新 $W^{l},b^{l}$

也就是：

$$v_{dW}=\beta v_{dW}+(1-\beta)dW \\ v_{db}=\beta v_{db}+(1-\beta)db \\ W=W-\alpha v_{dW} , b=b-\alpha v_{db}$$

原理解释

我们在之前就讲到了minibatch的缺点在于摆动 ，取加权平均数可以可以有效减小摆动

注意：

1. $\beta$ 一般默认设置为0.9
2. $v_{dW}$ 初始设置应为 和 $dW$ 形状相同的零矩阵，$v_{db}$ 初始设置应为 和 $db$ 形状相同的零矩阵

（3）代码实现

动量梯度下降算法 属于 步骤 4：训练过程（Training Loop），优化器（Optimizer）

PyTorch 已经自带 SGD + Momentum：

optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)

参数	含义
lr	学习率 α
momentum	动量系数 β，通常 0.9
weight_decay	L2 正则化，可选

for epoch in range(num_epochs):
    model.train()                         # 切换到训练模式，启用 Dropout，启用 BatchNorm 的训练状态
    for images, labels in train_loader:   # 每次循环处理一个 minibatch
        outputs = model(images)           # 前向传播
        loss = criterion(outputs, labels)  

        optimizer.zero_grad()             # 梯度清零
        loss.backward()                   # 反向传播，自动计算出模型所有参数的 `.grad`
        optimizer.step()                  # 根据 `.grad` 更新模型参数，用的更新策略是你定义的 optimizer

代码解释

outputs = model(images)

输入 images，通过模型计算出预测结果 outputs

• 对于分类问题：通常是 softmax 概率
• 对于二分类：通常是 sigmoid 概率
• 对于回归：直接是预测值

loss = criterion(outputs, labels)

• 计算 损失函数 loss
  • criterion 是你定义的 loss 函数，比如：
    • nn.CrossEntropyLoss() → 多分类
    • nn.BCELoss() → 二分类
    • nn.MSELoss() → 回归
  • 把 outputs 和真值 labels 比较，算出 loss

（三）RMSprop 算法

（root mean square prop算法）

RMSprop 算法 和 动量梯度下降算法Momentum 非常相似，都可以减小摆动，加快逼近速度，允许使用更大的学习率

只是计算方法有一点点不一样，具体如下：

$$S_{dW}=\beta S_{dW}+(1-\beta)dW^2 \\ S_{db}=\beta S_{db}+(1-\beta)db^2 \\ \\ W = W-\alpha \frac {dW}{\sqrt{S_{dW}}+10^{-8}} , b = b-\alpha \frac {db}{\sqrt{S_{db}}+10^{-8}}$$

注意：

1. 这个平方的操作是针对这一整个符号的
2. $+10^{-8}$ 是为了防止分母趋近于0

代码实现

RMSprop 算法属于 步骤 4：训练过程（Training Loop），优化器（Optimizer）

optimizer = torch.optim.RMSprop(model.parameters(), lr=0.001, alpha=0.99, eps=1e-08)

参数	含义	推荐值
lr	学习率 α	0.001
alpha	衰减系数 β（历史平方平均）	0.9 ~ 0.99
eps	防止除零	1e-8

for epoch in range(num_epochs):
    model.train()
    for images, labels in train_loader:
        outputs = model(images)
        loss = criterion(outputs, labels)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()  # 自动用了 RMSprop 算法更新

（四）Adam优化算法

Adam优化算法就是将 Momentum 和 RMSprop 结合在一起

具体算法如下：

在第 t 次迭代中

$$v_{dW}=0 \\ S_{dW}=0 \\ v_{db}=0 \\ S_{db}=0 \\ -------------------\\ v_{dW}={\beta}_1 v_{dW}+(1-{\beta}_1)dW \\ v_{db}={\beta}_1 v_{db}+(1-{\beta}_1)db \\ S_{dW}={\beta}_2 S_{dW}+(1-{\beta}_2)dW^2 \\ S_{db}={\beta}_2 S_{db}+(1-{\beta}_2)db^2 \\ -------------------\\ \\ v_{dW}^{corrected}=v_{dW}/(1-{\beta}_1^t) \\ v_{db}^{corrected}=v_{db}/(1-{\beta}_1^t) \\ S_{dW}^{corrected}=S_{dW}/(1-{\beta}_2^t) \\ S_{db}^{corrected}=S_{db}/(1-{\beta}_2^t) \\ -------------------\\ W = W-\alpha \frac {v_{dW}^{corrected}}{\sqrt{S_{dW}^{corrected}}+10^{-8}} \\ b = b-\alpha \frac {v_{db}^{corrected}}{\sqrt{S_{db}^{corrected}}+10^{-8}}$$

注意：

1. 其中 ${\beta}_1$ 建议设置为0.9，${\beta}_2$ 建议设置为 0.999

关于 Momentum,RMSprop 和 Adam 算法能够加快收敛速度的解释：

首先对于比较大的神经网络而言，由于W参数很多，所以不太可能会困在局部最优解，因为这要求很多参数同时为凹函数或者凸函数

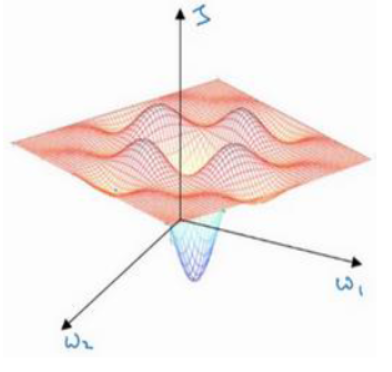
真正影响收敛速度的是下面这种鞍形。在鞍中点的斜率也是0

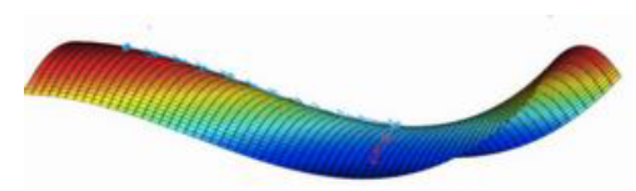
如果鞍的中间区段比较缓的话，这段时间的收敛就会很慢

而使用这些算法，由于‘动量’很大，所以可以快速地度过这些区域

Adam 的优点

• 学习率自动调整
• 收敛速度快
• 不需要太多调参
• 是深度学习中 最常用优化器之一
• 它内部会动态调整学习率（lr），自动平滑梯度（Momentum 一阶/二阶）

代码实现

Adam 优化算法 属于步骤 4：训练过程（Training Loop） → 优化器 Optimizer

optimizer = torch.optim.Adam(model.parameters(), lr=0.001, betas=(0.9, 0.999), eps=1e-8)

参数	含义	推荐值
lr	学习率 α	0.001
betas	β1,β2	(0.9, 0.999)
eps	防止除零	1e-8

for epoch in range(num_epochs):
    model.train()
    for images, labels in train_loader:
        outputs = model(images)
        loss = criterion(outputs, labels)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()  # 这里 step() 用的是 Adam 更新

（五）学习率衰减

（Learning Rate Decay）

由于学习率 $\alpha$ 是固定值，所以最后可能无法完全收敛到最优解，而是在最优解附近摆动。

这就需要我们让学习率不断降低，来收敛到最优解

所以对a的修改如下：

$$a=\frac{1}{1+decayrate*epoch\_num} a_0$$

其中：

• $a_0$为初始学习率

• epoch_num 是当前是第几个 epoch

• decayrate 是衰减率，也是一个超参数

代码实现

学习率衰减（Learning Rate Decay）属于 步骤 4：训练过程（Training Loop）→ 优化器 + Scheduler 学习率调度器

$$\alpha_t = \frac{1}{1 + \text{decayrate} \times \text{epoch}} \cdot \alpha_0$$

这叫 Step Decay（epoch 级别调整）

用 torch.optim.lr_scheduler.LambdaLR 可以实现自定义 decay 规则：

optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

# 定义 decay 函数
lr_lambda = lambda epoch: 1 / (1 + decay_rate * epoch)

scheduler = torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda=lr_lambda)

在每个 epoch 结束后调用：

for epoch in range(num_epochs):
    model.train()
    for images, labels in train_loader:
        outputs = model(images)
        loss = criterion(outputs, labels)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
    
    # 更新学习率
    scheduler.step()

其他内置 decay 策略

Scheduler	策略
StepLR	每隔固定 epoch 乘以 γ
ExponentialLR	每个 epoch 按 γ 指数衰减
ReduceLROnPlateau	监控 val_loss，当不提升时衰减 lr
CosineAnnealingLR	余弦退火