第 4 课：深层神经网络的优化

对 Pytorch 框架的重要说明

从这章开始，我们的代码实现都会通过 Pytorch 完成。

用 PyTorch 实现神经网络项目，标准流程基本都可以分为以下五个主要步骤：

1. 数据集定义（Dataset）

• 通常通过继承 torch.utils.data.Dataset，实现自定义的数据读取逻辑。
• 负责从磁盘读取图片/文本/CSV等原始数据，并返回张量和标签。

2. 数据加载与预处理（DataLoader & Transform）

• 使用 torch.utils.data.DataLoader 实现批量加载、打乱顺序、并行加速等。
• 利用 torchvision.transforms 或自定义方法对数据进行缩放、归一化、增强等预处理。

3. 神经网络架构（Model/Network）

• 通过继承 torch.nn.Module，定义网络的各层结构和前向传播逻辑（forward）。
• 可以是MLP、CNN、RNN等任意结构。

4. 训练过程（Training Loop）

• 包括前向传播、损失计算、反向传播、参数更新等步骤。
• 需要设置损失函数（如 nn.CrossEntropyLoss、nn.BCELoss）、优化器（如 optim.Adam、optim.SGD）等。
• 通常会有多轮（epoch）训练，并可输出损失、准确率等指标。

5. 测试过程（Evaluation/Testing）

• 切换到 model.eval() 模式，关闭梯度计算。
• 在测试集上前向传播，统计预测准确率或其他评价指标。

总结：
这五个步骤是 PyTorch 乃至大多数深度学习框架的标准流程。
无论是图像、文本还是其他类型任务，基本都可以套用这套结构，只需根据具体任务调整细节即可。

因此下面我们的优化步骤都是针对其中某一个步骤的

（一） 训练集，验证集和测试集

(train\Dev\test sets)

一般把收集到的数据按照 6 : 2 ：2 的比例分配。但是对于非常大体量的数据而言，验证集和测试集占比例会更小。

同时，应当尽可能保持 验证集和测试集 相似，防止出现问题

如果数据量不够，没有测试集也没有关系

（二）偏差和方差

（Bias\Variance）

有三种情况：

• 欠拟合（underfitting）：高偏差（high bias）

• 过拟合（overfitting）： 高方差（high variance）

• 适度拟合（just right）

如何判断是哪种情况呢？
假设最优误差是0% （最优误差又称为贝叶斯误差，是人眼识别的误差）

情况	训练集误差	测试集误差	描述
过拟合（高方差）	1%	15%	过拟合，模型在训练集上表现很好但在测试集上表现较差，说明模型过于复杂，对训练数据过度敏感。
欠拟合（高偏差）	15%	16%	欠拟合，模型在训练集和测试集上都表现不佳，说明模型过于简单，无法捕捉基本趋势。
高偏差+高方差	15%	30%	模型在训练集上的误差较高，并且在测试集上误差更大，说明模型既不能准确捕捉趋势也无法泛化到新数据。
适度拟合	1%	2%	适度拟合，模型在训练集和测试集上都表现很好，误差低且相差不大，说明模型泛化能力强。

总之：训练集的误差决定是否是 高偏差，测试集和训练集的准确率差异大小决定是否是 高方差
注意：如果最优误差不是0%，而是比如15%，那么这里的第二种情况也可以算作是 适度拟合

方差和偏差是在优化算法中最基本的衡量指标：

第一步：判断是否高偏差（是否成功拟合）

• 如果偏差偏高：

  1. 使用更深更复杂的网络
  2. 增加训练时间
  3. 使用更先进的优化算法
  4. 使用NN卷积神经网络

• 当偏差正常之后，进行第二步：

第二步: 判断是否高方差（是否过拟合）

• 如果方差偏高：
  1. 增加数据量
  2. 正则化（Regularization）
  3. 使用NN卷积神经网络

（三）正则化

（Regulation）

正则化主要有两种：L2正则化 和 dropout机制

其实还有 L1 正则化，但是性能不如 L2 所以就不介绍了

1. L2 正则化

L2 正则化 属于 步骤 4 ：训练过程（Training Loop） 里 → 损失函数 J(w, b) 定义部分**

• 最终的 loss = 原始_loss + 正则项
• 在训练循环里，每次计算 loss 时一起计算出来

对于单个节点而言，之前我们对成本函数的定义如下：

$$J(w, b) = \frac{1}{m} \sum_{i=1}^m L(\hat{y}^{(i)}, y^{(i)})$$

现在修改如下：

$$J(w, b) = \frac{1}{m} \sum_{i=1}^{m} L({\hat y}^{(i)}, y^{(i)}) + \frac{\lambda}{2m} \|w\|_2^2 \\ ||w||_2^2 = \sum_{j=1}^{n_x} w_j^2 = w^T w$$

注意：

1. $||w||_2$是向量参数 w 的欧几里得范数（也就是L2范数），算法如上。 $||w||_1$是 L1 范数，算法改成 $\sum_{j=1}^{n_x} |w_j|$
2. $\lambda$ 是正则化参数，需要慢慢试出来，也是一个超参数

神经网络中的L2正则化：

$$J(w^{(1)}, b^{(1)}, \ldots, w^{(L)}, b^{(L)}) = \frac{1}{m} \sum_{i=1}^m L(\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2m} \sum_{l=1}^L \|w^{(l)}\|_F^2 \\ \|w^{(l)}\|_F^2 = \sum_{i=1}^{n^{(l-1)}} \sum_{j=1}^{n^{(l)}} (w_{ij}^{(l)})^2$$

注意：

1. 之前讲过 $W^{[l]}$的形状是 $(n^{[l]},n^{[l-1]})$
2. 该矩阵范数被称为弗罗贝尼乌斯范数，用下标F表示

对于 L2 正则化，其反向传播（BackProp）如下：

$$\frac{\partial J}{\partial w} = \frac{\partial L}{\partial w} + \frac{\lambda}{m} w \\ dW = \text{From backprop} + \frac{\lambda}{m} w \\ w := w - \alpha dW$$

注意:

1. 显而易见，W被减去的更多了，所以L2正则化又叫 权重衰减（Weight Decay）
2. From backprop 是通过反向传播算法计算得到的权重的梯度,也就是上一部分中已经算出的部分
3. $\lambda$ 的取值方法：

• 小型模型和/或大型数据集：尝试 $10^{-7}$ 到 $10^{-5}$
• 大型模型和/或小型数据集：尝试 $10^{-5}$ 到 $10^{-3}$

代码实现

• L2 正则化（Weight Decay）—— PyTorch 优化器直接支持

  optimizer = torch.optim.Adam(model.parameters(), lr=1e-3, weight_decay=1e-5)
  

  其中 weight_decay 就是对应的 L2 正则 λ。

• L1 正则化（需要手动加）

  L1 正则 PyTorch 没有 weight_decay 参数，要自己加在 loss 里：

  # 假设在训练循环里
  model.train()
  for X_batch, y_batch in train_loader:
      optimizer.zero_grad()
      
      outputs = model(X_batch)
      original_loss = criterion(outputs, y_batch)
      
      # L1 正则化
      l1_lambda = 1e-5
      l1_norm = sum(p.abs().sum() for p in model.parameters())
      loss = original_loss + l1_lambda * l1_norm
      
      loss.backward()
      optimizer.step()
  

2. Dropout 正则化

Dropout 会遍历网络的每一层，并随机从这一层中消除某几个节点。每一层都要设置一个保留节点的概率（比例），各个层设置的比例可以不一样。这种随机“关闭”神经元的效果是，网络不能依赖于任何一个神经元，因为它可能在任何训练轮次中被关闭。 这迫使网络分散学习信息，从而增加其泛化能力。

如何实现dropout呢？我们以一个层数 L=3 的神经网络为例

1. 设计一个具体数字 keep_prob，大小为 0~1，表示保留某个隐藏单元的概率。下面的案例中被设置为0.8，表示为每个节点有0.8的概率被保存

2. 然后定义d，$d^{[3]}$ 表示一个3层的dropout向量

   keep_prob=0.8
   d3=np.random.rand(a3.shape[0],a3.shape[1])< keep_prob
   

   • d3 是一个与 a3 （某层的激活输出）同形状的布尔矩阵，其中的每个元素都是通过比较一个随机数（从均匀分布中抽取）和 keep_prob 获得的。

   • 如果随机数小于 keep_prob，相应位置的值为 True（意味着该神经元在这次迭代中保持激活），否则为 False（神经元输出被置为0）

3. 接下来更新a3，直接把a3和d3相乘，让$d^{[3]}$中的为0的元素和$a^{[3]}$中的对应元素归零

a3=np.multiply(a3,d3)
#python会自动把True和False转化为1和0
a3/=keep_prob  # 最后向外拓展a3

为什么要除keep_prob呢？

因为 a3 中已经有20%的节点被删除了，为了不影响Z4的期望值，a3要除以0.8来修正或弥补所需的那20%, 使Z4的期望值不变

dropout机制一般在正向传播中使用，并且每训练一次就要 dropout 一次

但是在对应的反方向传播的每一层也要使用 对应相同的 dropout mask 进行处理

注意：

1. 当keep_prob被设置为1时，就关闭了dropout机制
2. 在测试阶段，不需要使用dropout
3. 对于节点数比较多的层，把keep_prob设置的小一点（多删一点），反之设置的大一点
4. 除非算法过拟合，否则不使用 dropout
5. dropout机制的一大缺点是代价函数J不能被再明确定义

代码实现

Dropout 正则化 属于 第 3 步：神经网络架构（Model/Network） 定义阶段

因为：

• Dropout 是一种 结构性正则化手段
• 它是定义在网络层内部的操作，属于 forward() 过程中的一部分
• 每轮训练过程中，Dropout 自动启用；而在测试阶段 model.eval()，Dropout 自动关闭

它不是在 loss 那里手动加项的正则化（像 L1/L2），而是写在 model 的结构里

以一个定义 MLP用于 二分类任务 的例子：

输入层：784 维 (例如 28x28 图片展开成 784 维向量)
↓
[ Linear(784 → 256) + ReLU + Dropout(p=0.2) ]
↓
[ Linear(256 → 128) + ReLU + Dropout(p=0.5) ]
↓
[ Linear(128 → 1) + Sigmoid ]
↓
输出层：1 维，表示类别概率（适合二分类）

import torch
import torch.nn as nn

class MLP(nn.Module):
    def __init__(self):
        super(MLP, self).__init__()
        self.fc1 = nn.Linear(784, 256)
        self.relu1 = nn.ReLU()
        self.dropout1 = nn.Dropout(p=0.2)  # keep_prob = 0.8
        self.fc2 = nn.Linear(256, 128)
        self.relu2 = nn.ReLU()
        self.dropout2 = nn.Dropout(p=0.5)  # keep_prob = 0.5
        self.fc3 = nn.Linear(128, 1)
        self.sigmoid = nn.Sigmoid()
        
    def forward(self, x):
        x = self.fc1(x)
        x = self.relu1(x)
        x = self.dropout1(x)  # Dropout 使用
        x = self.fc2(x)
        x = self.relu2(x)
        x = self.dropout2(x)  # Dropout 使用
        x = self.fc3(x)
        x = self.sigmoid(x)
        return x

• 训练阶段：model.train()，Dropout 启用
• 测试阶段：model.eval()，Dropout 关闭

3. 正则化的意义

L2正则化使部分权重被衰减，Dropout机制直接删除了部分节点，所以都是简化了网络，但是缺没有减少深度，所以防止了过拟合

同时，由于sigmoid和tanh函数中间部分更接近于线性。而当W变小时，Z也会变小，所以会更接近函数的中间部分，也就是接近线性。而线性层的叠加是不会增加复杂度的。

（四）其他正则化方法

除了上面说到的L2正则化和Dropout之外，还有几种正则化方法

方法一：人工图片扩增

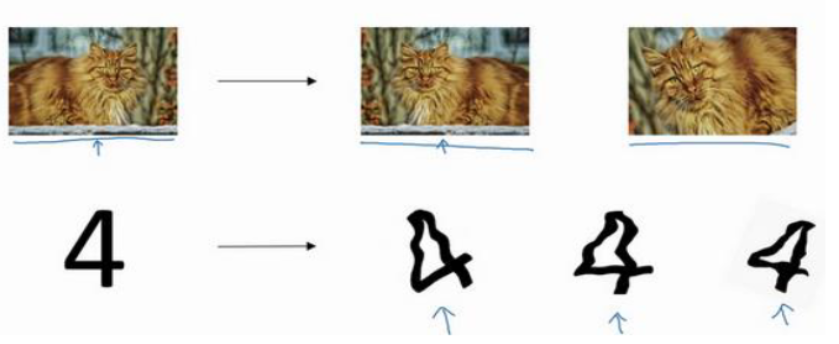
也就是 transforms数据增强， 代码实现可以参考这个笔记：[第 4 课：数据加载（中） | HeiheT09 的技术笔记](http://notes.heihet09.com/docs/AI/Pytorch教程/第 4 课：数据加载（中）#一-transforms数据增强)

方法二：Early Stopping

图中蓝线代表训练集误差，紫线代表测试误差 。通过及时停止训练，来防止过拟合

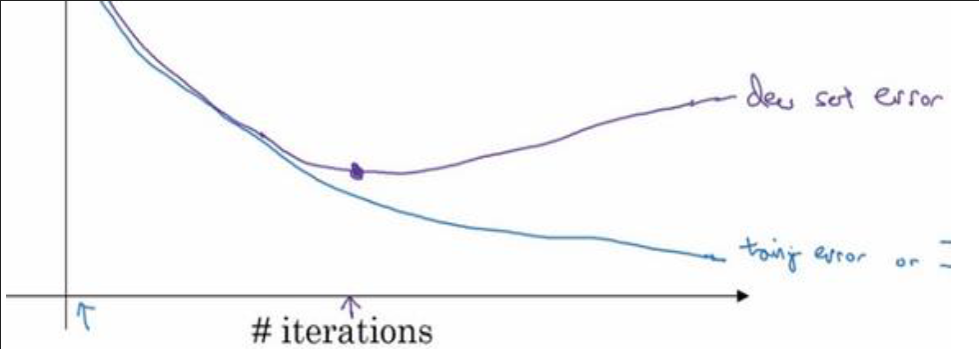
但是这种方法有一个缺点：

就是不能独立地处理这两个问题，因为提早停止梯度下降，也就是停止了优化代价函数J，

因为现在你不再尝试降低代价函数，所以代价函数J的值可能不够小，同时你又希望不出现过拟合，

你没有采取不同的方式来解决这两个问题，而是用一种方法同时解决两个问题，这样做的结果是我要考虑的东西变得更复杂。

Early stopping 的优点是，只运行一次梯度下降，你可以找出 𝑤的较小值，中间值和较大值，而无需尝试 𝐿2正则化超级参数 𝜆的很多值。

Early Stopping 作用

• 防止过拟合
• 节省训练时间
• 保留效果最好的模型

代码实现

Early Stopping 属于 第 4 步：训练过程（Training Loop）

• Early Stopping 是监控验证集的 loss / metric，如果连续多轮没有提升，就提前停止训练
• 它是 训练阶段的一个“停止策略”
• 不是定义模型结构（不是步骤 3），也不是 loss 本身（不是 L1/L2）

# 参数
patience = 10  # 最多允许多少个 epoch 没提升
best_loss = float('inf')
epochs_no_improve = 0

for epoch in range(num_epochs):
    model.train()
    train_loss = 0.0
    
    for images, labels in train_loader:
        # 训练循环同前
        ...
        train_loss += loss.item() * images.size(0)
    
    train_loss /= len(train_loader.dataset)
    
    # ----------- 验证集 -------------
    model.eval()
    val_loss = 0.0
    
    with torch.no_grad():
        for images, labels in val_loader:
            outputs = model(images)
            loss = criterion(outputs, labels)
            val_loss += loss.item() * images.size(0)
    
    val_loss /= len(val_loader.dataset)
    print(f'Epoch {epoch+1}/{num_epochs}, Train Loss: {train_loss:.4f}, Val Loss: {val_loss:.4f}')
    
    # ----------- Early Stopping -------------
    if val_loss < best_loss:
        best_loss = val_loss
        epochs_no_improve = 0
        # 可选：保存当前最优模型
        torch.save(model.state_dict(), 'best_model.pth')
    else:
        epochs_no_improve += 1
        print(f'No improvement for {epochs_no_improve} epochs')
    
    if epochs_no_improve >= patience:
        print(f'Early stopping triggered after {epoch+1} epochs')
        break

tip

torch.save(model.state_dict(), 'best_model.pth') 会保存成什么？

它保存的是： ✅ 仅保存 模型的“参数字典”（state_dict） ✅ 不是整个 model 代码结构！

model.state_dict() → 是一个 Python 的 dict

{
    'layer1.weight': tensor(...),
    'layer1.bias': tensor(...),
    'layer2.weight': tensor(...),
    ...
}

也就是说：

• 保存的是模型里每一层的参数（权重 weight + 偏置 bias）
• 以 层名 → 参数 Tensor 的映射保存下来
• .pth 是常见习惯扩展名，文件本质是 二进制序列化后的字典

保存阶段：

torch.save(model.state_dict(), 'best_model.pth')

加载阶段（未来重新加载模型）：

model = MLP()  # 重新创建模型结构
model.load_state_dict(torch.load('best_model.pth'))
model.to(device)
model.eval()  # 切换到评估模式

如果要保存“整个模型”怎么办？可以这样：

torch.save(model, 'whole_model.pth')

但是这种方式保存的是整个模型 + 结构代码（Pickle），移植性差

（五）归一化输入

（Normalizing inputs）

这个方法用于加速训练

假设一个训练集有两个特征（输入特征为2维），归一化需要两个步骤：

1. 把均值降到0
2. 归一化方差

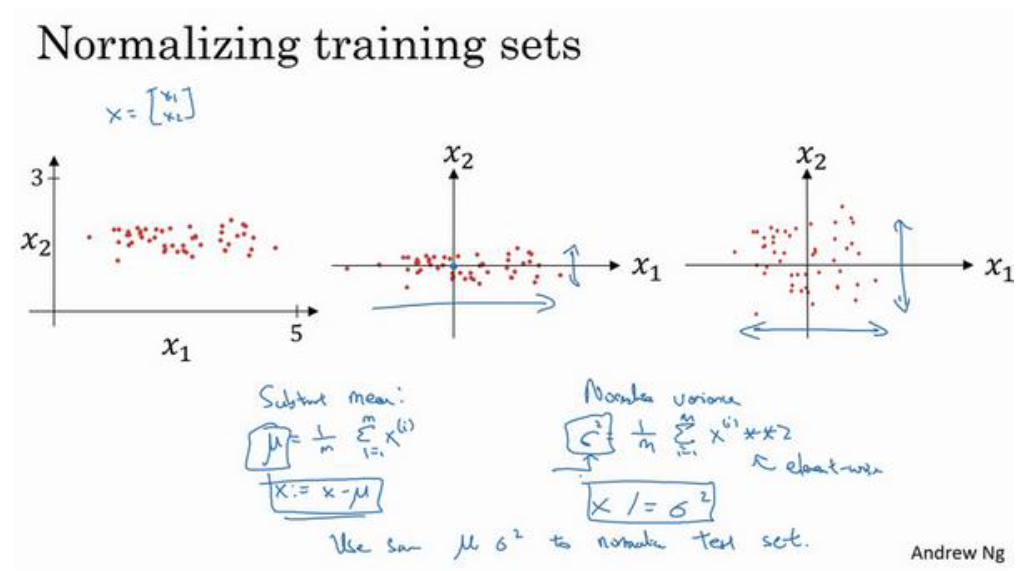
归一化的目的是将输入数据转换为统一的尺度，帮助优化算法（如梯度下降）更快地收敛到最小损失

$$X_{\text{std}} = \frac{X - \mu}{\sigma}$$

其中 $\mu$ 是特征的均值，$\sigma$ 是特征的标准差。

$$\mu = \frac{1}{m} \sum_{i=1}^m x_i$$ $$\sigma = \sqrt{\frac{1}{m} \sum_{i=1}^m (x_i - \mu)^2}$$

注意：

1. 其中 m 是特征值的数量，$x_i$ 是每个特征值。
2. 这种转换后，特征集 X 的新均值将是0，标准差将是1，即 $X_{\text{std}}$ 的所有值都围绕0分布，具有单位方差。
3. 要用同样的方法调整测试集，而不是在训练集和测试集上分别预估 𝜇 和 𝜎2。

也就是说测试集使用的 𝜇 和 𝜎2 也是由训练集数据计算得来的。

为什么要归一化输入呢？

可以看下图中的代价函数3维图形（注：这些数据轴应该是 𝑤1和 𝑤2）

如上图所示，优化前必须要使用比较小的学习率（步长），但是优化后成本函数更圆，所以可以使用更大的学习率

注意：

1. 这里的更快不是指计算更快。而是指可以使用更大的学习率，更快达到最优点
2. 当 x1,x2,x3 的大小范围比较相似时，用不用归一化其实差别不大。但是如果大小范围差别很大，归一化特征值就非常重要了。
3. 执行这类归一化并不会产生什么危害，所以可以都加上

代码实现

归一化操作 属于 第 2 步：数据加载与预处理（DataLoader & Transform）

归一化是 在数据送入模型之前做的预处理， 目的是优化模型训练过程（加速收敛 / 提升效果）

应该放在 Dataset / DataLoader 阶段，写在 transform 里

图像归一化（典型做法）

from torchvision import transforms

# 假设是 3 通道图像
transform = transforms.Compose([
    transforms.ToTensor(),  # 把 PIL Image 转成 Tensor，值变成 [0,1]
    transforms.Normalize(mean=[0.5, 0.5, 0.5], std=[0.5, 0.5, 0.5])  # 归一化
])

也可以用 训练集算出来的 mean/std：

mean = [0.4914, 0.4822, 0.4465]
std = [0.2023, 0.1994, 0.2010]

transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize(mean=mean, std=std)
])

表格数据 / tabular data 归一化

可以用 sklearn：

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)  # 🚨 注意：用训练集的 μ 和 σ

（六）梯度消失/梯度爆炸

（Vanishing/Exploding gradients）

在训练深度神经网络时，有时坡度会变得非常大或者非常小。梯度爆炸是因为在极深的神经网络中，某一个位置的权重经过反复的乘法，出现了指数爆炸的现象 。梯度消失的原理也是一样的

要解决这个问题，需要研究一下 *神经网络的权重初始化*

在神经网络中，线性组合的计算公式为：

$$Z = w_1x_1 + w_2x_2 + \ldots + w_nx_n，b = 0，$$

暂时忽略 𝑏，为了预防 𝑧值过大或过小， 所以当 𝑛 越大时，我们希望 $\omega_i$ 越小，

所以权重$w_i$的初始化公式为：

$$w_i = \frac{1}{n}$$

其中，$n$是神经元的输入数量。

在Python中，可以使用numpy库如下初始化第$[l]$层的权重：

$$W[l] = np.random.randn(shape) * np.sqrt(\frac{1}{n^{[l-1]}})$$

1. He初始化

属于 步骤 3：模型结构（Model/Network）

适用场景：

• 激活函数用 ReLU / LeakyReLU / PReLU
• 深层网络

原理：

• 让每一层的方差保持稳定
• 避免前向/反向传播时出现梯度消失/爆炸

数学（Normal 分布版）：

$$w \sim \mathcal{N} \left( 0, \frac{2}{n_{\text{in}}} \right)$$

parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * np.sqrt(2. / layer_dims[l-1])  #He初始化

def init_weights_he(m):
    if isinstance(m, nn.Linear) or isinstance(m, nn.Conv2d):
        nn.init.kaiming_normal_(m.weight, mode='fan_in', nonlinearity='relu')
        if m.bias is not None:
            nn.init.constant_(m.bias, 0)
model = MLP()
model.apply(init_weights_he)  # He 初始化

2. Xavier初始化（Glorot 初始化）

属于 步骤 3：模型结构（Model/Network）

适用场景：

• 激活函数是 tanh / sigmoid（以前用得多，现在用得少）
• 层次不深的网络

数学（Normal 分布版）：

$$w \sim \mathcal{N} \left( 0, \frac{1}{n_{\text{in}}} \right)$$

parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * np.sqrt(1. / layer_dims[l-1])

def init_weights_xavier(m):
    if isinstance(m, nn.Linear) or isinstance(m, nn.Conv2d):
        nn.init.xavier_normal_(m.weight)
        if m.bias is not None:
            nn.init.constant_(m.bias, 0)
model = MLP()
model.apply(init_weights_xavier)  # Xavier 初始化