第 3 课：深层神经网络

（一）深度神经网络的介绍

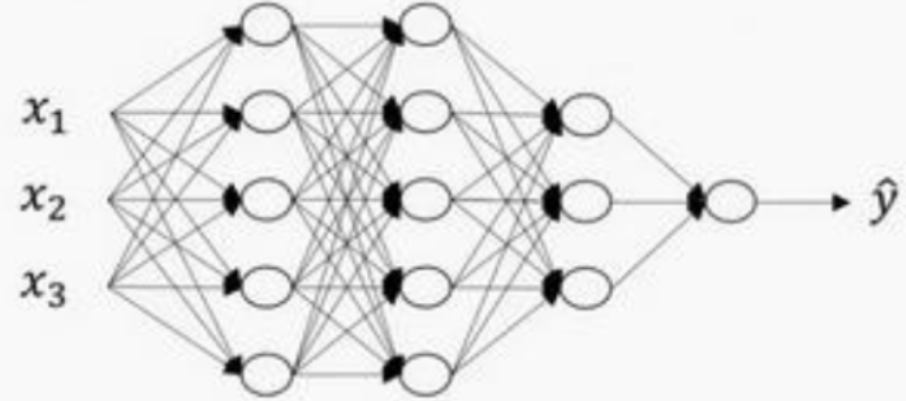
上图中我们看到一个典型的四层神经网络，对于每一层的节点数，可以这样表示：

$$L=4 ， n^{[0]}=n^x=3 , n^{[1]}=5 , n^{[2]} =5 , n^{[3]}=3 ， n^{[4]}=n^{[L]}=1$$

每一层l的激活函数记为 $a^{[l]}$, 其中第0层的 $X=a^{[0]}$

下图解释了深度神经网络的内在机制，浅层隐藏层会去识别边缘，中层隐藏层识别部分特征，深层隐藏层可以构建一张完整人脸

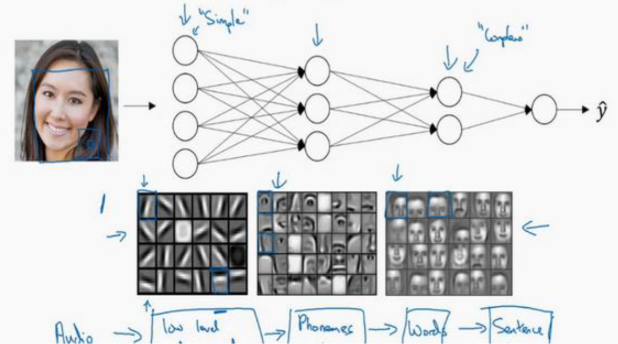
这种原理对于语言识别等神经网络也是适用的，比如浅层神经元处理小的音调升降，中间神经元识别音位（比如元音辅音），深层神经元识别单词，再形成词组，句子等

另外，相比于浅层神经网络，想要得到相同的计算结果，深层神经网络需要的总节点数量 比浅层神经网络 要少非常非常多（尤其是对于规模比较大的计算）

（二）深度神经网络的正向和反向传播

对于l层而言：

正向传播：

$$Z^{[l]} = W^{[l]} A^{[l-1]} + b^{[l]}$$ $$A^{[l]} = g^{[l]}(Z^{[l]})$$

其中对于第一层而言 $A^{[l-1]}=A^{[0]}$ 就是$X$

反向传播：

$$dz^{[l]} = da^{[l]} \ast g'^{[l]}(z^{[l]}) \\ dw^{[l]} = dz^{[l]} \cdot a^{[l-1]} \\ db^{[l]} = dz^{[l]} \\ da^{[l-1]} = (w^{[l]})^T \cdot dz^{[l]} \\$$

向量化之后如下：

$$dZ^{[l]} = dA^{[l]} \ast g'^{[l]}(Z^{[l]}) \\ dW^{[l]} = \frac{1}{m} dZ^{[l]} \cdot (A^{[l-1]})^T \\ db^{[l]} = \frac{1}{m} \text{np.sum}(dZ^{[l]}, \text{axis} = 1, \text{keepdims} = True) \\ dA^{[l-1]} = (W^{[l]})^T \cdot dz^{[l]} \\$$

整个计算流程如图

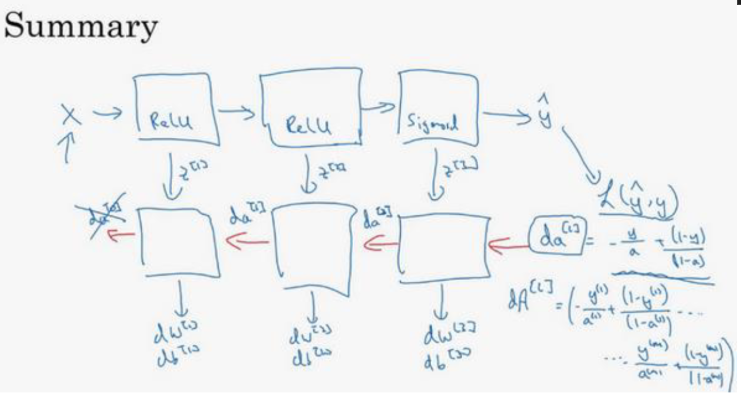
对于每一次训练，从X开始，向右正向传播，计算成本函数，然后反向传播

从计算过程中可以看出，反向传播中需要正向传播的相应环节传递参数$Z^{[l]}$

但是仔细观察参数，我们可以发现有一个参数似乎没有得到计算，反向传播的第一个$dA^{[L]}$

我们必须先算出这个值， 由于对于最后一层而言，

$$L(\hat{y},y) = -ylog(\hat{y})-(1-y)log(1-\hat{y})$$

其中$y$是真实标签，$\hat y$ 是预测概率，也就是$A^{[L]}$

所以要求的$dA^{[L]}$其实就是

$$dA^{[L]}=\frac{\partial L}{\partial A^{[L]}} = - \left( \frac{y}{A^{[L]}} - \frac{1 - y}{1 - A^{[L]}} \right)$$

用python表达式就是

dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))

（三）每一层的维度

$$b^{[l]} : (n^{[l]},1) \\ W^{[l]} : (n^{[l]},n^{[l-1]}) \\$$

$dW^{[l]}$和$W^{[l]}$的维度相同，$db^{[l]}$和$b^{[l]}$的维度相同

对于z和a而言：

向量化前：

$$Z^{[l]} : (n^{[l]},1) \\ A^{[l]} : (n^{[l]},1) \\$$

向量化后:

$$Z^{[l]} = (z^{[l](1)}, z^{ }, z^{ }, \ldots, z^{[l](m)}) \\ Z^{[l]} : (n^{[l]}, m) \\ A^{[l]}: (n^{[l]}, m) \\ A^{[0]} = X = (n^{[0]}, m)$$

（四）注意事项

1. 不是只有第一个W和b需要更新，每一个W和b都要更新！这样才是每一个神经元都得到训练！

2. 对于深度神经网络，在初始化W的时候，不要再使用*0.01来初始化权重W的标准差，这会导致神经网络在训练初期就陷入较小的梯度值（梯度消失问题）， cost会一直收敛在0.693147，也就是-log(0.5)。对于 ReLU 激活函数，建议使用 He初始化。 He初始化 有助于神经网络更快地收敛。这是因为它避免了权重在训练初期过小或过大，这些极端值可能会导致学习过程缓慢或不稳定。

3. 对于深度神经网络，仅仅是100张照片是远远不够的，虽然理论上可以用很少的图片（如几百张）来训练一个模型，但这通常会导致模型性能不佳或者过拟合。有些来源建议至少需要1000张图片每个类别来训练一个稳健的模型 。数据的多样性和质量同样重要。不仅需要数量足够，还需要保证数据能够覆盖到类别的各种变化，包括不同的环境、角度、光照条件等。

4. 0.6931471就是没有成功学习的表现

（五）代码实现

from PIL import Image
import numpy as np
import os

（1）数据加载

# 数据加载模块
def img2array(file_path,size):
    try: 
        image = Image.open(file_path)  
        image = image.resize(size)  
        image_array = np.array(image) / 255.0  # 转化成array，并且除以 255 进行数据标准化方法。
        # 神经网络训练时，较小的数值范围（如 0 到 1）可以帮助模型更快地收敛，因为大的数值范围或极端值可能会导致训练过程中的数值不稳定。
        # 同时因为sigmoid函数在z很大的时候会变得很平缓，所以小一点会训练快一点
        if image_array.shape[2] != 3:  # 确认是RGB格式
            print("图片不是RGB格式")
            return None
        else:
            image_array = image_array.reshape(-1, 1)  # -1指自动计算这个维度应该有多少元素。1制定了只有一列
            # print(f"{file_path}处理完成，准备好用于模型输入")
            return image_array
    except Exception as e:
        print(f"Error processing {file_path}: {str(e)}")
        return None

def load_pictures(folder_path,size):
    X = np.empty((size[0]*size[1]*3, 0))  # 行数不变（每一张照片都是64**2*3个元素），列数可以变（逐个加载照片）
    Y = np.empty((1, 0))  # 行数不变（每一张照片只有一个结果，是不是猫），列数可以变（逐个加载照片）
    file_list = [file for file in os.scandir(folder_path) if file.is_file()]
    m=len(file_list)

    for file in file_list:
        file_path = os.path.join(folder_path, file.name)
        img_array = img2array(file_path,size)

        if img_array is not None:
            X = np.hstack((X, img_array)) 
            if 'cat' in file.name:
                Y = np.hstack((Y, np.array([[1]])))  
            else:
                Y = np.hstack((Y, np.array([[0]])))  

    print('所有图片处理完成')
    print('————————————————————————————————————————————————————————————————————————————————————————')
    return X, Y,m

（2）定义神经网络

# 数学函数模块
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def sigmoid_d(z):
    return sigmoid(z)*(1-sigmoid(z))

def tanh(z):
    return (np.exp(z)-np.exp(-z))/(np.exp(z)+np.exp(-z))

def tanh_d(z):
    return 1-tanh(z)**2

def ReLU(z):
    return np.maximum(0,z)  #注意不要使用内置的max！

def ReLU_d(Z):  #注意不要用if else判断语句，不然是不能进行批量操作的
    return np.where(Z > 0, 1, 0)

# 神经网络核心代码
def compute_cost(A, Y):
    m = Y.shape[1]  # m是样本数
    A = np.clip(A, 1e-8, 1 - 1e-8)  # 防止log(0)
    cost = -np.sum(Y * np.log(A) + (1 - Y) * np.log(1 - A)) / m
    cost = np.squeeze(cost)  # 确保成本是标量
    return cost

# 值负责核心计算功能的向前传播函数
def forward_propagation(A, W, b,activation_func):   
    Z = np.dot(W, A) + b
    A = activation_func(Z)
    return A, Z

# 管理所有向前传播细节的函数
def forward_propagation_complete(X,Y, parameters,chosen_func,Z_cache,A_cache): 

    A = X
    L = len(parameters) // 2   #总层数 是 W和b的总数的一半
    A_cache['A0']=X

    for l in range(1, L+1):
        A_prev = A
        func=chosen_func[l]
        W=parameters['W' + str(l)]
        b=parameters['b' + str(l)]
        A, Z = forward_propagation(A_prev, W , b, func)


        A_cache['A'+str(l)]=A
        Z_cache['Z'+str(l)]=Z
    
    cost=compute_cost(A, Y)
    
    return A_cache,Z_cache,cost

def backward_propagation(dA, Z, A, W, activation_func_d,m):
    dZ = dA * activation_func_d(Z)
    dW = np.dot(dZ, A.T) / m
    db = np.sum(dZ, axis=1, keepdims=True) / m
    dA_prev = np.dot(W.T, dZ)
    return dW, db, dA_prev

def backward_propagation_complete(X,Y, parameters,chosen_func_d,Z_cache,A_cache,dW_cache,db_cache):
    m = X.shape[1]
    
    L = len(parameters) // 2   #总层数 是 W和b的总数的一般
    AL=A_cache.get('A'+str(L))
    dA= - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))


    for l in range(L,0,-1):
        
        Z=Z_cache.get('Z'+str(l))
        prev_A=A_cache.get('A'+str(l-1))
        W=parameters['W' + str(l)]
        activation_func_d=chosen_func_d[l]
        
        dW,db,dA=backward_propagation(dA,Z,prev_A,W,activation_func_d ,m)

        dW_cache['dW'+str(l)]=dW
        db_cache['db'+str(l)]=db
    

    return dW_cache,db_cache

def update_parameters(parameters, dW_cache, db_cache, learning_rate):
    L = len(parameters) // 2
    for l in range(1, L+1):
        parameters['W' + str(l)] -= learning_rate * dW_cache['dW' + str(l)]
        parameters['b' + str(l)] -= learning_rate * db_cache['db' + str(l)]
    return parameters

func_list={
    1:sigmoid,
    2:tanh,
    3:ReLU,

    0:None
}
func_d_list={
    1:sigmoid_d,
    2:tanh_d,
    3:ReLU_d,

    0:None
}

（3）训练过程

# 超参数
size=(64,64)     #图片压缩后的大小
dim=size[0]*size[1]*3  #图片的输入形状 64*64*3
layer_dims = [dim,20,10, 5, 1]  # 本参数可以任意修改隐藏层数和每个层的节点数
func_choose=[0,3,3,3,1]       # 本层可以设置每层的激活函数，除了第一层没有激活函数是None
learning_rate=0.01
num_iterations=2000

# 加载数据
train_path = '/home/heihe/Machine_learning/deep-learning/data/cat_dog_2/train'
test_path = '/home/heihe/Machine_learning/deep-learning/data/cat_dog_2/test'

X, Y, m = load_pictures(train_path,size)  #m是训练样本数，Y是标注集，X是训练集
print("X shape:", X.shape)
print("Y shape:", Y.shape)

所有图片处理完成
————————————————————————————————————————————————————————————————————————————————————————
X shape: (12288, 1002)
Y shape: (1, 1002)

# 随机初始化模块

def initialize_parameters_deep(layer_dims):
    parameters = {}
    number_of_layers = len(layer_dims)
    for l in range(1, number_of_layers):
        parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * np.sqrt(2. / layer_dims[l-1])  #He初始化
#       parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * 0.01   
        parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
    return parameters

# 获得初始化参数 
parameters=initialize_parameters_deep(layer_dims)  
chosen_func=[func_list.get(i) for i in func_choose] 
chosen_func_d=[func_d_list.get(i) for i in func_choose] 
print(chosen_func)
print(chosen_func_d)

[None, <function ReLU at 0x7f20cc2af380>, <function ReLU at 0x7f20cc2af380>, <function ReLU at 0x7f20cc2af380>, <function sigmoid at 0x7f20cc2af100>]
[None, <function ReLU_d at 0x7f20cc2af420>, <function ReLU_d at 0x7f20cc2af420>, <function ReLU_d at 0x7f20cc2af420>, <function sigmoid_d at 0x7f20cc2af1a0>]

#核心控制模块
def train(X, Y, num_iterations, learning_rate ,parameters,chosen_func,chosen_func_d):
    A_cache={}
    Z_cache={}
    dW_cache={}
    db_cache={}

    costs=[]

    L = len(parameters) // 2   #总层数 是 W和b的总数的一般
    
    for i in range(num_iterations):
        A_cache,Z_cache,cost=forward_propagation_complete(X,Y, parameters,chosen_func,Z_cache,A_cache)
        dW_cache,db_cache=backward_propagation_complete(X,Y, parameters,chosen_func_d,Z_cache,A_cache,dW_cache,db_cache)
        parameters=update_parameters(parameters,dW_cache,db_cache,learning_rate)
        
        if i % 100 == 0:  #每训练100次输出一次
            costs.append(cost)
            print(f"Cost after iteration {i}: {cost}")


    return parameters, costs

parameters, costs = train(X, Y, num_iterations, learning_rate ,parameters,chosen_func,chosen_func_d)  #训练2k次，每次的步长为0.005

Cost after iteration 0: 0.9737703803732627
Cost after iteration 100: 0.6753364467508026
Cost after iteration 200: 0.6487641241322979
Cost after iteration 300: 0.5913118590591449
Cost after iteration 400: 0.6179804821912424
Cost after iteration 500: 0.6059088343463981
Cost after iteration 600: 0.5973947735160478
Cost after iteration 700: 0.5914504166643055
Cost after iteration 800: 0.5571737557951916
Cost after iteration 900: 0.6259221521316449
Cost after iteration 1000: 0.5748125220734608
Cost after iteration 1100: 0.5353735336047871
Cost after iteration 1200: 0.47935136841986037
Cost after iteration 1300: 0.42522308423333344
Cost after iteration 1400: 0.7026927900308567
Cost after iteration 1500: 0.3619838919110616
Cost after iteration 1600: 0.3677645703368401
Cost after iteration 1700: 0.3564116603150527
Cost after iteration 1800: 0.49423198275948055
Cost after iteration 1900: 0.4244990151934811

（4）测试过程

# 测试模块

def test(X_test, parameters,chosen_func,m_test): #管理所有向前传播细节的函数
    Y_prediction = np.zeros((1, m_test))

    A = X_test
    L = len(parameters) // 2   #总层数 是 W和b的总数的一般

    for l in range(1, L+1):
        A_prev = A
        activation_func=chosen_func[l]
        W=parameters['W' + str(l)]
        b=parameters['b' + str(l)]


        Z = np.dot(W, A_prev) + b
        A = activation_func(Z)

    for i in range(A.shape[1]):
        Y_prediction[0, i] = 1 if A[0, i] > 0.5 else 0  
        # 把Y_predict中大于0.5的改成1，否则改成0，用于表示每一个最终预测结果
    
    # 这里的for循环可以使用下面这一行代替
    # Y_prediction = (A2 > 0.5).astype(int)

    return Y_prediction

#测试准确度
# 册数数据集中，全是猫的图片，用来检测二分类准确性 
X_test, Y_test, m_test = load_pictures(test_path,size)
Y_prediction = test(X_test, parameters,chosen_func,m_test)
print(f"Accuracy: {np.mean(Y_prediction == Y_test)*100}%")
# 逐个元素进行比较是否相同，结果是一个布尔值数组。布尔值 True 可以被当作 1 处理，False 被当作 0。
print("Test finished.")

所有图片处理完成
————————————————————————————————————————————————————————————————————————————————————————
Accuracy: 54.45544554455446%
Test finished.

（六）Pytorch 介绍

在上面的手搓代码实现中，我们可以注意到随着神经网络的结构变得复杂，代码的实现难度变得很大。因此接下来的教程，我们都将使用 Pytorch 框架来快速构建神经网络。

基础教程移步这里：Intro | HeiheT09 的技术笔记

import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader
from torchvision import transforms
from PIL import Image
import os

1. 数据集定义

# 自定义Dataset
class CatDogDataset(Dataset):
    # 初始化，读取文件夹下所有图片文件名，保存到 `self.file_list`，并保存预处理方法transform
    def __init__(self, folder_path, transform=None):
        self.folder_path = folder_path
        self.transform = transform
        self.file_list = [f for f in os.listdir(folder_path) if os.path.isfile(os.path.join(folder_path, f))]
    
    # 返回数据集的图片数量
    def __len__(self):
        return len(self.file_list)
    
    # 根据索引读取图片，转为RGB格式，应用预处理，并根据文件名判断标签（文件名含cat为1，否则为0）。
    def __getitem__(self, idx):
        img_name = self.file_list[idx]
        img_path = os.path.join(self.folder_path, img_name)
        image = Image.open(img_path).convert('RGB')
        if self.transform:
            image = self.transform(image)
        label = 1 if 'cat' in img_name else 0
        return image, label

2. 数据加载与预处理

• train_dataset、test_dataset：

• DataLoader：用于，，。

transform = transforms.Compose([   # 将多个预处理操作组合起来
    transforms.Resize((64, 64)),   # 先将图片缩放到64x64
    transforms.ToTensor(),         # 再转为张量（范围0~1）
])

train_path = '/home/heihe/Machine_learning/deep-learning/data/cat_dog_2/train'
test_path = '/home/heihe/Machine_learning/deep-learning/data/cat_dog_2/test'

# 创建自定义数据集对象，自动读取图片和标签。
train_dataset = CatDogDataset(train_path, transform=transform)
test_dataset = CatDogDataset(test_path, transform=transform)

# 批量加载数据
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True) # batch_size=32表示每次取32张图片
test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False)  # shuffle=True表示训练集每轮打乱顺序

3. 神经网络架构

解释：这是一个多层感知机（MLP）模型，继承自nn.Module。

• nn.Flatten()：将输入的多维图片（3x64x64）展平成一维向量（12288）。

• nn.Sequential：按顺序堆叠各层。（包含3个全连接层）

​ 第一层：12288 → 256，激活函数 ReLU。

​ 第二层：256→64，激活函数 ReLU。

​ 第三层：64→1，激活函数 Sigmoid（输出概率）。

• forward：定义前向传播过程。

class MLP(nn.Module):
    def __init__(self):
        super(MLP, self).__init__()
        self.flatten = nn.Flatten()
        self.model = nn.Sequential(
            nn.Linear(64*64*3, 256),
            nn.ReLU(),
            nn.Linear(256, 64),
            nn.ReLU(),
            nn.Linear(64, 1),
            nn.Sigmoid()
        )
    def forward(self, x):
        x = self.flatten(x)
        x = self.model(x)
        return x

4. 训练过程

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') # 自动检测是否有GPU，有则用GPU加速。
model = MLP().to(device)                                 # 实例化模型并转到设备上
criterion = nn.BCELoss()                                 # 二分类交叉熵损失函数
optimizer = optim.Adam(model.parameters(), lr=0.001)     # Adam优化器，学习率0.001

num_epochs = 200                                         # 训练200轮
count = 0
for epoch in range(num_epochs):
    model.train()                                        # 设置为训练模式。
    running_loss = 0.0
    for images, labels in train_loader:                  # 遍历训练集的每个batch：
        images = images.to(device)                       # 图片和标签转到设备上，
        labels = labels.float().unsqueeze(1).to(device)  # 标签变成float并扩展为二维（[batch, 1]）。
        outputs = model(images)	                         # 前向传播
        loss = criterion(outputs, labels)                # 计算损失
        optimizer.zero_grad()
        loss.backward()                                  # 反向传播
        optimizer.step()                                 # 更新参数
        running_loss += loss.item() * images.size(0)     # 累加损失。
    epoch_loss = running_loss / len(train_loader.dataset)
    count += 1
    if count % 50 == 0:                                  # 每50轮输出一次平均损失。
        print(f'Epoch {epoch+1}/{num_epochs}, Loss: {epoch_loss:.4f}')

输出

Epoch 50/200, Loss: 0.3043
Epoch 100/200, Loss: 0.1633
Epoch 150/200, Loss: 0.0066
Epoch 200/200, Loss: 0.0006

5. 测试过程

model.eval()                                           # 设置为评估模式，关闭Dropout/BN等
correct = 0
total = 0
with torch.no_grad():                                  # 关闭梯度计算，节省内存和加速推理
    for images, labels in test_loader:
        images = images.to(device)
        labels = labels.to(device)
        outputs = model(images)                        # 前向传播，得到输出概率。
        predicted = (outputs > 0.5).squeeze(1).long()  # outputs > 0.5：概率大于0.5判为猫（1），否则为狗（0）
        correct += (predicted == labels).sum().item()  # 统计预测正确的数量。
        total += labels.size(0)                        # 统计总数。
print(f'测试集准确率: {100 * correct / total:.2f}%')

测试集准确率: 66.34%