第 1 课:二分类神经网络
(一)样本的数据结构
一张已经被标记为“xxx”的图 被称作样品
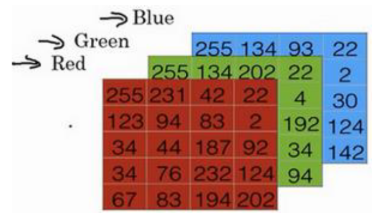
图像由形状(长度,高度,深度=3)的3D阵列表示。然而,当您读取图像作为算法的输入时,您可以将其转换为形状为(长度 * 高度* 3,1)的向量。换句话说,可以将三维阵列“展开”或重塑为一维矢量。也就是把3个图层的数据连起来排成一列,成为一个
具体方法如下:
def image2vector(image):
a=image.shape[0]
b=image.shape[1]
c=image.shape[2]
v=image.reshape(a*b*c,1)
return v
处理好图像后,得到向量x作为输入变量
输入
: 表示一个 维度特征,为输入特征,维度为 。
输出
: 表示输出结果,取值为 ;
: 表示第 组数据,可能是训练数据,也可能是测试数据,此处暂译为训练数据;
: 表示不同的训练数据组成的输入矩阵,放在一个 的矩阵中;
: 对应训练不同训练数据组成的输出矩阵,维度为 。
表示测试集的时候,我们会用 来默认表示 ,而测试集 需要单独注明:
(二)逻辑回归
对于二元分类问题来说,给定一个输入特征向量 ,它可能属于一类或另一类,模型的任务就是找出其属于哪一类。
我们的模型在计算过程中,需要将输入特征 转换为输出估计值 。
比如对于猫图而言,如果“是猫图”的 表示为 1, “不是猫图”的 表示为 0
那么 需要在(0,1)之内,表示“是猫图”的可能性
在开始之前,我们先介绍一下用sigmoid函数来处理向量x
sigmoid函数的导数为:
import numpy as np
def sigmoid(x):
s=1/(1+np.exp(-x))
return s
def sigmoid_derivative(x):
ds=sigmoid(x)*(1-sigmoid(x))
return ds
接下来就是预测的模型
Given , 而我们希望 .
如何来衡量模型的准确性呢?
需要用到 “损失函数”(loss function):
-
当 y=1 时,只有 尽可能大(收范围限制趋近于1),损失函数L才会小
-
当 y=0 时,只有 尽可能小(收范围限制趋近于0),损失函数L才会小
然而这只是对于一个样本的衡量方法,对于一个样本集而言,需要进行累加,这称为 成本函数(Cost Function)
那么现在优化的方向就已经相当明确了,我们要不断修改w和b来让成本函数尽量小
而事实上,使用了sigmoid 函数,这个成本函数是有最低点的
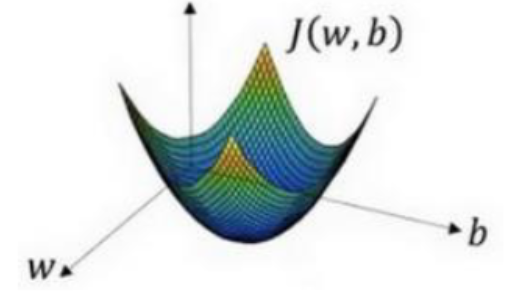
所以直接使用 *梯度下降法*:
假设b不变时:
其中
𝑎 :学习率( learning rate)
: 步长 (step),即向下走一步的长度
注意:
对于 我们一般简写做
拓展到两个参数就是:
(三)逻辑回归中的梯度下降
(Logistic Regression Gradient Descent)
我们在前面已经了解了逻辑回归的训练过程
那么怎么计算 和 呢?
假设样本有2个特征 ,那么 z 的表达式应该修改为:
回忆一下:
其损失函数为:
对于单个样本而言,代��价函数 就是损失函数:
其中 𝑎 是逻辑回归的输出, 𝑦 是样本的标签值
求导可得:
同时:
因为:
同时,我们一般直接用 来表示
因为:
所以:
因为:
综上,对于单个样本的梯度下降算法:
其中
上述结论拓展到m个样本应该如何呢?
我们知道:
即:
其中 是第 i 个样本的预测输出,是第 i 个样本的实际标签。
对权重 () 的梯度:
对权重 () 的梯度:
对偏置 () 的梯度:
梯度下降更新规则
使用上述计算出的平均梯度来更新参数:
其中, 是学习率,用于控制更新步骤的大小。
(四)向量化
在上面的计算方法中,每进行一次梯度下降时,都需要使用for循环来遍历每一个样本。 事实上这样的效率非常低,所以我们学习使用 向量化(Vectorization) 来解决这个问题
所谓向量化,就是对于一串数据,比如数组或者矩阵,本来采用for循环进行一个个的运算,
但是现在使用numpy库的自带功能,去掉显式的for循环
import numpy as np
import time
data = np.random.rand(1000000) # 假设有一个大型数组
# 向量化计算平方根和平均值
tik = time.time()
sqrt_data_vectorized = np.sqrt(data)
tok = time.time()
time1 = tok - tik
print('time:', time1)
print(sqrt_data_vectorized[:5]) # 打印前5个元素作为示例
# 普通计算方法
tik = time.time()
sqrt_list = [] # 使用列表收集平方根结果
for i in data:
sqrt_list.append(i**0.5) # 向列表追加平方根
sqrt_data = np.array(sqrt_list) # 将列表转换为NumPy数组
tok = time.time()
time2 = tok - tik
print('time:', time2)
print(sqrt_data[:5]) # 打印前5个元素作为示例
上面的结果可以看到相差了100多倍
所谓向量化,不一定要调用numpy的计算函数比如 np.mean() np.sqrt()等,而是使用了np.array 的数据格式
比如对于一个 np.array 进行 **2 平方操作,也是向量化的
根据我们已经学会的算法,可以知道现在的计算过程如下:
初始化 , , , 。代码流程如下:
J = 0; dw1 = 0; dw2 = 0; db = 0
for i in range(1, m+1): # 假设m是样本数量
z_i = w * x[i] + b # 这里假设x[i]是一个包含x1和x2的向量
a_i = sigmoid(z_i)
J += -[y[i] * log(a_i) + (1 - y[i]) * log(1 - a_i)]
dz_i = a_i - y[i]
dw1 += x[i][0] * dz_i # 假设x[i][0]是特征x1
dw2 += x[i][1] * dz_i # 假设x[i][1]是特征x2
db += dz_i
# 外部循环结束后,计算平均值
J /= m
dw1 /= m
dw2 /= m
db /= m
# 更新参数
w1 = w1 - alpha * dw1
w2 = w2 - alpha * dw2
b = b - alpha * db
上面这段代码中实现了一次梯度下降,也就是一次训练,但是使用了两个循环
第一个循环是for循环遍历每一个样本
第二个循环是对特征值进行循环。在这例子我们有 2 个特征值。如果你有超过两个特征时,需要循环 𝑑𝑤1 、 𝑑𝑤2 、 𝑑𝑤3 等等。
我们先来看第二个循环的向量化
不用初始化 都等于 0,而是定义 𝑑𝑤 为一个向量,设置 定义一个行的一维向量
其中 代表单个样本的特征数,对于一张图片而言可能是 64* 64 *3
而其实 dw 不需要专门在代码开头初始化,因为 dw 是根据w自动算出来的,形状也是取决于w

再来看 第一个循环的向量化
回忆一下最开始讲到的输入集
: 表示不同的训练数据组成的输入矩阵,放在一个 的矩阵中;
:单个样本的特征点数,对于图片而言可能是 64 * 64 * 3
: 对应训练不同训练数据组成的输出矩阵,维度为 。
表示测试集的时候,我们会用 来默认表示 ,而测试集 需要单独注明:
所以先计算 ,把他们都放到一个 的行向量中
你可以发现他可以表达为 (w的转置)
是一个 的行向量
所以计算的最终得到的是一个 的向量,,计算方式为 ,其中
其中,
-
是向量 的第一个元素,
-
是第二个元素,
-
以此类推,直到 是第 个元素。
Z=np.dot(w.T, X)+b
其中b通过广播机制自动被拓展成一个 的行向量
加下来要使用向量Z计算出向量Y
: 对应训练不同训练数据组成的输出矩阵,维度为 。
然后就可以计算
对偏置 (b) 的梯度:
所以
db=(1/m)*np.sum(dZ)
对权重 (w) 的梯度:
所以
(五)总结
这是没有使用向量化的计算过程

这是使用向量化之后�的计算过程
(六)注意事项
这里要讲一个重要且常见的bug——一维数组
import numpy as np
a=np.random.rand(5)
print(a.shape) #(5,)
# 此时a就是一个一维数组,既不是行向量也不是列向量
这种结构很容易出现意想不到的bug,所以是要坚决摈弃的,一定要修改成(5,1)
import numpy as np
a=np.random.rand(5,1)
print(a.shape) #(5,1)
(七)完整代码
from PIL import Image
import numpy as np
import os
(1) 加载图片
数据加载模块
def img2array(file_path):
try:
image = Image.open(file_path)
image = image.resize((64, 64))
image_array = np.array(image) / 255.0 # 转化成array,并且除以 255 进行数据标准化方法。
# 神经网络训练时,较小的数值范围(如 0 到 1)可以帮助模型更快地收敛,因为大的数值范围或极端值可能会导致训练过程中的数值不稳定。
# 同时因为sigmoid函数在z很大的时候会变得很平缓,所以小一点会训练快一点
if image_array.shape[2] != 3: # 确认是RGB格式
print("图片不是RGB格式")
return None
else:
image_array = image_array.reshape(-1, 1) # -1指自动计算这个维度应该有多少元素。1制定了只有一列
# print(f"{file_path}处理完成,准备好用于模型输入")
return image_array
except Exception as e:
print(f"Error processing {file_path}: {str(e)}")
return None
def load_pictures(folder_path):
X = np.empty((12288, 0)) # 行数不变(每一张照片都是64**2*3个元素),列数可以变(逐个加载照片)
Y = np.empty((1, 0)) # 行数不变(每一张照片只有一个结果,是不是猫),列数可以变(逐个加载照片)
file_list = [file for file in os.scandir(folder_path) if file.is_file()]
m=len(file_list)
for file in file_list:
file_path = os.path.join(folder_path, file.name)
img_array = img2array(file_path)
if img_array is not None:
X = np.hstack((X, img_array))
if 'cat' in file.name:
Y = np.hstack((Y, np.array([[1]])))
else:
Y = np.hstack((Y, np.array([[0]])))
return X, Y,m
train_path = "/home/heihe/Machine_learning/deep-learning/data/dog_cat/train"
test_path = "/home/heihe/Machine_learning/deep-learning/data/dog_cat/test"
X, Y, m = load_pictures(train_path) #m是训练样本数,Y是标注集,X是训练集
print("样本数 m:", m)
print("X shape:", X.shape)
print("Y shape:", Y.shape)
输出
样本数 m: 32
X shape: (12288, 32)
Y shape: (1, 32)
(2)训练模块
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def optimize(w, b, X, Y,learning_rate): #单次传播(也就是一次优化)
m = X.shape[1] #训练样本数
Z = np.dot(w.T, X) + b
A = sigmoid(Z)
cost = (-1/m) * np.sum(Y * np.log(A) + (1-Y) * np.log(1-A)) #计算本次所有的损失
dZ = A - Y
dw = (1/m) * np.dot(X, dZ.T)
db = (1/m) * np.sum(dZ)
w = w - learning_rate * dw
b = b - learning_rate * db
return w, b, dw, db, cost
# 核心控制模块
def train(w, b, X, Y, num_iterations, learning_rate, print_cost=False):
costs = []
for i in range(num_iterations):
w, b ,dw, db, cost = optimize(w, b, X, Y,learning_rate)
if i % 100 == 0: #每训练100次输出一次
costs.append(cost)
if print_cost:
print(f"Cost after iteration {i}: {cost}")
return w, b, dw, db, costs
# 初始化参数
dim=12288 #单张图片的大小64*64*3
w = np.zeros((dim, 1))
b = 0
final_w, final_b, final_dw, final_db, costs = train(w, b, X, Y, num_iterations=2000, learning_rate=0.005, print_cost=True) #训练2k次,每次的步长为0.005
print("Optimization finished.")
输出
Cost after iteration 0: 0.6931471805599453
Cost after iteration 100: 0.18530029860345393
Cost after iteration 200: 0.1090077322566628
Cost after iteration 300: 0.07617812647876984
Cost after iteration 400: 0.05819557281243573
Cost after iteration 500: 0.046939662625746885
Cost after iteration 600: 0.03926500479225721
Cost after iteration 700: 0.03371166698439108
Cost after iteration 800: 0.02951398408604718
Cost after iteration 900: 0.026233278927329164
Cost after iteration 1000: 0.023600782933165858
Cost after iteration 1100: 0.02144292456815562
Cost after iteration 1200: 0.019642750450395985
Cost after iteration 1300: 0.018118653827904823
Cost after iteration 1400: 0.016811999787415703
Cost after iteration 1500: 0.015679597101431735
Cost after iteration 1600: 0.014688941877837529
Cost after iteration 1700: 0.01381511329893244
Cost after iteration 1800: 0.013038689737581223
Cost after iteration 1900: 0.012344314914233732
Optimization finished.
(3)测试模块
def test(w, b, X,m):
Y_prediction = np.zeros((1, m))
Z = np.dot(w.T, X) + b
A = sigmoid(Z)
for i in range(A.shape[1]):
Y_prediction[0, i] = 1 if A[0, i] > 0.5 else 0
# 把Y_predict中大于0.5的改成1,否则改成0,用于表示每一个最终预测结果
return Y_prediction
测试准确度
册数数据集中,全是猫的图片,用来检测二分类准确性
X_test, Y_test, m_test = load_pictures(test_path)
Y_prediction = test(final_w, final_b, X_test,m_test)
print("Accuracy:", np.mean(Y_prediction == Y_test))
print("Optimization finished.")